Matematické Fórum

check_drummer · 06. 01. 2011 19:25

Ahoj,
existuje teorie, která pomůže při řešení hlavolamu typu Rubikovy kostky? Nejspíš teorie grup. Konkrétní problém, který mám, je (mluvme o Rubikově kostce, ale analogii lze použít i na ostatní hlavolamy podobného typu):

Pro hlavolam existuje několik povolených operací jak z jednoho stavu hlavolamu přejít do jiného (např. otočení pravé stěny o 90 stupňů) - tyto operace jsou permutacemi nad množinou kostiček (plošek) Rubikovy kostky - označme množinu těchto permutací P. S každou permutací je v P obsažena i permutace inverzní (která "vrací" hlavolam do původního stavu).

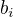Popis situace a problému: Hlavolam je "částečně" složen, tj. některé kostičky jsou umístěny na svých místech, ovšem některé nikoli. Úkol zní - umístit na svá místa některé z dosud neumístěných kostiček aniž by došlo k narušení již správně umístěných kostiček. Tedy: Nechť je dána množina správně umístěných kostiček K a prvky $a_i$ a $b_i$ (jejichž význam je: správná pozice kostičky (ve složeném hlavolemu) nyní umístěné na místě $a_i$ je na místě $b_i$ ). 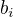Úkolem je najít takovou posloupnost operací z P (označme ji p), že p(x)=x pro všechna x z K a 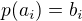$p(a_i)=b_i$ pro všechna i. (Po tomto kroku můžme K rozšířit o správně umístěné kostičky 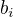$b_i$ a pokračovat iterativně znovu v umísťování dalších kostiček.)

Existuje však nějaká teorie, které by pomohla tento problém vyřešit - namísto zkusmého zkoušení hledání řešení?

Děkuji za příspěvky

Kondr · 11. 01. 2011 21:14

Stavy kostky tvoří stavový prostor. Nejhloupější, co můžeme udělat, je procházet do šířky (najdeme nejkratší řešení, ale za dlouho). Lepší je použít nějaký heuristický algoritmus, třeba A*, kde metriku postavíme na počtu správně umístěných kostiček.

Pokud nám nejde o optimální řešení, tak prostě najdeme posloupnosti tahů, které dělají na kostce jen lokální změny (prohození dvou kostek třeba) a z těch řešení poskládáme.

Pokud se bavíme o rubikově kostce, třeba pomůže http://cube20.org/ .

petrkovar

Ideální by bylo, kdybychom uměli najít posloupnost několika operací, které změní stav jediné kostky. To však obvykle není možné (třeba u Rubikovy kostky se musí vždy pohnout aleposň dvě kostičky). Myslím, že proto Kondr zmiňuje posloupnosti, které dělají na kostce lokální změny: co nejméně ovlivněných kostek. Z těch pak jako z kuchařky (pamětníci je pamatují pro Rubikovu kostku) můžeme poskládat libovolnou přípustnou kombinaci.
Jak takové posloupnosti tahů najít? To není lehké, jinak by úplná diskuze Rubikovy kostky nedala tolik práce. Myslím, že bez vhodného algebraického softwaru (jako magma) to už pro malé hlavolamy nemusí být ručně řešitelné.

Dana1 · 17. 01. 2011 12:37 — Editoval Dana1 (17. 01. 2011 12:38)

↑ check_drummer:
Prepáč, úplne OT: nemá byť v tom nadpise témy slovo hlavolamů ? Alebo je to naschvál?

check_drummer · 18. 01. 2011 17:28

↑ Dana1:
Děkuji, překlep. :-)

Matematické Fórum

#1 06. 01. 2011 19:25

Řešení hlavovalů typu "Rubikova kostka"

#2 11. 01. 2011 21:14

Re: Řešení hlavovalů typu "Rubikova kostka"

#3 11. 01. 2011 21:26 — Editoval petrkovar (11. 01. 2011 21:27)

Re: Řešení hlavovalů typu "Rubikova kostka"

#4 17. 01. 2011 12:37 — Editoval Dana1 (17. 01. 2011 12:38)

Re: Řešení hlavovalů typu "Rubikova kostka"

#5 18. 01. 2011 17:28

Re: Řešení hlavovalů typu "Rubikova kostka"

Zápatí