Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Burnsideovo lemma: Počet dvoubarevných náhrdelníků
#1 14. 01. 2011 19:58
Burnsideovo lemma: Počet dvoubarevných náhrdelníků
Zdravím. Při písemce z algebry jsem dneska potkal příklad, který se mi nepovedlo tak úplně vyřešit, ač mi připadá, že potřebnou teorii mám vzládnutou.
Zadání je: Kolika způsoby je z osmi korálků možné sestavit náhrdelník, kde přesně pět korálků je bílých a tři jsou černé. Přičemž dvě sestavení náhrdelníku se považují za totožné pokud je jedno z druhého možné dostat rotací nebo zrcadlením. Navíc dodám, že náhrdelník jde dokolečka, nepočítá se rozepnutý náhrdelník.
Řešit se to má algebraicky přes počet orbit, tedy Burnsideovým lemmatem.
Tedy jsem si řekl, že budu barvit oněch osm korálků na náhrdelníku. Vezmu množinu X = mna všech obarvení osmi korálků. Formálně,  , kde 1 (v oboru hodnot) značí bílý korálek, 0 černý. Je
, kde 1 (v oboru hodnot) značí bílý korálek, 0 černý. Je  , protože každé obarvení získám tak, že si řeknu, kterých pět z oněch osmi korálků má být bílých, zbylé nechám černé.
, protože každé obarvení získám tak, že si řeknu, kterých pět z oněch osmi korálků má být bílých, zbylé nechám černé.
Potud věřím, že jsem počítal dobře. Dál si přestávám být trošku jistý.
Potřebuju grupu rotací a zrcadlení. Zvolil jsem 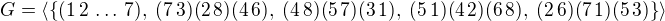 .Tedy grupu generovanou těmito prvky, což jsou permutace v cyklickém zápisu.
.Tedy grupu generovanou těmito prvky, což jsou permutace v cyklickém zápisu.
První prvek generující G by měl generovat všechny možné rotace náhrdelníku. Od zbylých čtyř prvků v mně generátorů bych rád, aby generovaly zrcadlení. Přišel jsem k nim tak, že jsem si nakreslil osmiúhelník s vrcholy 1, 2, ..., 8 a pak permutacemi vyjádřil zrcadlení okolo os 1-5, 2-6, 3-7 a 4-8. (Pořadí odpovídá pořadí v zápisu mny generátorů.)
Formálně potřebuju akci G na X. Vzal jsem 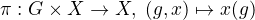 . Tady se mi trošku nezdá, že se tam prohazuje pořadí x a g. Myslím si ale, že to má být tak, protože potřebuju, aby výsledkem byla fce
. Tady se mi trošku nezdá, že se tam prohazuje pořadí x a g. Myslím si ale, že to má být tak, protože potřebuju, aby výsledkem byla fce 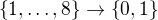 , což
, což 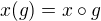 je.
je.
Chci určit počty pevných bodů každého prvku z G. Pro id se každé x zobrazí samo na sebe, tedy 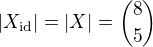 .
.
Pro libovolnou rotaci si myslím, že žádný pevný bod není. Neumím to ale dokázat pořádně. Myšlenka je taková, že všechny tři černé korálky se musí zobrazit na stejné místo -- černé korálky jsou ale přesně tři, takže jediná možnost by byla, kdyby byly uspořádané na rovnostranném trojúhelníku, jehož vrcholy jsou vrcholy výše zmíněného pravidelného osmiúhelníku. Takový ale neexistuje, tedy žádná rotace nemá žádný pevný bod.
Pro každé zrcadlení by mělo existovat šest pevných bodů. Opět se budu odvolávat na osmiúhelník. Vezmu zrcadlení okolo nějaké osy, třeba 1-5. Pak si můžu vybrat, která z dvojic (8 2), (7 3), (6, 4) bude mít oba vrcholy černé -- to můžu zvolit třemi způsoby. Nakonec si zvolím jeden vrchol na osce zrcadlení, který bude též černý -- to můžu udělat dvěma způsoby.
Nakonec potřebuju velikost grupy G. Obsahuje identitu, sedm rotací, čtyři zrcadlení a navíc se zrcadlení a rotace můžou skládat dohromady. Což dává 1 + 4 . 7 = 29 prvků. (Věřím, že tohle číslo je špatně.)
Po dosazení do Burnsideova lemmatu dostávám očividně chybný výsledek: 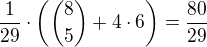 .
.
Můj kámen úrazu, myslím, není ani tak v algebře samotné, jako spíš ve výčtu všech možností při zrcadlení a otáčení. Takže uvítám, když se tu najde někdo ochotný vysvětlit, kde a jak vzít potřebná čísla.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#2 14. 01. 2011 21:22
Re: Burnsideovo lemma: Počet dvoubarevných náhrdelníků
Několik postřehů:
Rotaci bych zapsal cyklem  .
.
Protože se jedná o dihedrální grupu n-úhelníka, tak zkušeného počtáře zarazí, že zrcadlení jsou jen4, když rotací je 8. Zapoměl jsi na zrcadlení, jejichž osa prochází středem hrany.
Složením dvou zrcadlení dostaneme otočení, složením dvou otočení zase otočení a složením otožení a zrcadlení zase zrcadlení. Všech prvků je stále 1+7+8=16 (já bych psal 8+8 a identitu v celkovém počtu považoval za otočení). Pro neidentickou rotaci pevný bod nenajdeme. Odpovídal by podgrupě, jejíž řád 3 by dělil 8. To není možné.
Zrcaldení přes středy hran nemají žádný pevný bod. To bychom museli mít počet prvků každé barvy sudý. Zrcadlení, kdy osa prochází je správně spočítáno.
Celkem dostaneme 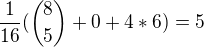 .
.
Offline
#3 16. 01. 2011 18:15
Re: Burnsideovo lemma: Počet dvoubarevných náhrdelníků
↑ petrkovar:
Ta rotace skutečně měla být (1 2 ... 8), jenom jsem napsal něco jiného, než jsem myslel.
Pro neidentickou rotaci pevný bod nenajdeme. Odpovídal by podgrupě, jejíž řád 3 by dělil 8. To není možné.
Tohle je moc hezký argument. Nevidím ale, jak se z takového pevného bodu dá vyrobit podgrupa řádu 3.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#4 16. 01. 2011 21:15
Re: Burnsideovo lemma: Počet dvoubarevných náhrdelníků
↑ Oxyd:Celá PODgrupa rotací má 8 prvků. Já chápu pevný bod tak, že použití nějaké rotace zachová obarvení korálků. Opakováním stejné rotace dostaneme opět identické obarvení korálků atd. Máme tři černé korálky a když je rotace neidentická, přechází použitím zmíněné rotace každý jeden z těchto korálků v nějaký jiný téže barvy. Sestavujeme cyklickou podgrupu. Jakého řádu? Neřádu 1, protože rotace je netriviální. Ne řádu 2, kam by se otočil třetí korálek? Řád tři by šel, ale čtyři a více ne, protože už nemáme tolik černých korálků.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Burnsideovo lemma: Počet dvoubarevných náhrdelníků
