Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 05. 2008 14:59
- petulkacip
- Příspěvky: 38
- Reputace: 0
goniometrie
jsem ztracena, prosim o pomoc...
zapomnela jsem vsechna pravidla pro goniometricke rovnice, funkce apod..:(
zkousela jsem si to pripomenout vasi matematikou polopate, ale stale jsem nenasla logicke postupy k reseni prikladu...
vsechna reseni rovnice tvori mnozinu sin^2 2x > 0 tvori mnozinu
vsechna reseni rovnice sin^3 x = 1 jsou
vsechna x nalezi do <0;2pi> ktera vyhovuji rovnici sin^2 x - 1 = tg^2 x tvori mnozinu
prosim o postup a o vysvetleni, doufam ze z toho pochopim postup k ostatnim silenostem podobneho druhu.... dekuju moc!!!!
Offline
#3 05. 05. 2008 16:33
Re: goniometrie
↑ petulkacip:
ad) vsechna reseni nerovnice  tvori mnozinu?
tvori mnozinu?
Tak to vezmeme postupne:
vyraz 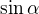 dava vysledky z intervalu
dava vysledky z intervalu  , to plati vzdy, i kdyz argumentem funkce sinus neni alfa, ale 2x.
, to plati vzdy, i kdyz argumentem funkce sinus neni alfa, ale 2x.
Po umocneni na druhou budou vysledky nezaporne, takze vyraz  dava vysledky z intervalu
dava vysledky z intervalu  , tj. vzdy plati, ze
, tj. vzdy plati, ze 
Tvym ukolem je ale zjistit, kdy plati jen VETSI NEZ NULA, takze staci, kdyz vyloucime vsechny pripady v nichz nastava varianta rovna se nule.
Z nerovnice proto resime tuto rovnici: odmocnim
odmocnim substituci t = 2x upravim do tvaru
substituci t = 2x upravim do tvaru z jednotkove kruznice nebo grafu vyplyva, ze
z jednotkove kruznice nebo grafu vyplyva, ze , tj.
, tj.  , kde
, kde  . Vratim se k puvodni promenne
. Vratim se k puvodni promenne delim 2
delim 2
Resenim nerovnice jsou vsechna realna cisla mimo celych nasobku pi/2
Offline
#4 05. 05. 2008 17:04
Re: goniometrie
ad) vsechna reseni rovnice  jsou?
jsou?
Jak je uvedeno vyse v prispevku od jarrro urcim treti odmocninu
urcim treti odmocninu z jednotkove kruznice nebo grafu plyne, ze
z jednotkove kruznice nebo grafu plyne, ze (z duvodu periodicnosti fce sinus).
(z duvodu periodicnosti fce sinus).
Tento vysledek po prevedeni scitancu na spolecneho jmenovatele a vytknuti pi/2 lze zapsat ve tvaru, jak uvedl jarrro, tj. .
.
Offline
#5 05. 05. 2008 17:21
Re: goniometrie
ad) vsechna x nalezi do  ktera vyhovuji rovnici
ktera vyhovuji rovnici  tvori mnozinu?
tvori mnozinu?
Na rozdil od predchozich rovnic ci nerovnic, zde je nutne uvazit i to, ze fce tangens neni definovana vzdy, ale k tomu se vratim az v raveru reseni.
Pro fci tangens pouziji vztah 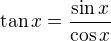 a dosadim do zadane rovnice.
a dosadim do zadane rovnice. 

Pokud to jde, snazim se mit v rovnici co nejmene fci, tady vyuziji goniometrickeho vztahu  a vyjadrim si fci kosinus jako
a vyjadrim si fci kosinus jako 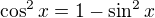 . Dosadim
. Dosadim
Zbavim se zlomku a po roznasobeni a prevedeni na jednu stranu prevedu na tvar:
Pokud se na vyraz 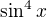 divame jako na
divame jako na  , tak po pouziti substituce
, tak po pouziti substituce  ziskame kvadratickou rovnici
ziskame kvadratickou rovnici
Jak si snadno overis, tato rovnice ma zaporny diskriminant a nema v oboru realnych cisel reseni. Takze ani zadana rovnice nema reseni a nemusime proto stanovovat, jake hodnoty x nelze kvuli fci tangens vubec dosadit.
Je to tak? Doufam, ze me nekdo kontroluje :-)
Offline
#6 06. 05. 2008 15:07
- petulkacip
- Příspěvky: 38
- Reputace: 0
Re: goniometrie
↑ Jorica: DEKUJU MOC, ted se snazim prijit na dalsi priklad..dokonce jsem si i namalovala graf, ale porad mi to nevychazi podle vysledku....
vsechna x nalezi do <0; 2pi>, ktera splnuji podminku |cos x/2| < nebo rovno 1/2 tvori mnozinu
prosim pekne o postup....
Offline
#7 08. 05. 2008 00:06
Re: goniometrie
↑ petulkacip:
No snad se mi to podari vysvetlit, je mozne, ze na to jdu zbytecne slozite.
Psala jsi, ze jsi kreslila graf, no ja mam radeji jednotkovou kruznici, ale na obrazku mas vpravo i graf.
Takze resime nerovnici 
Pokud to budu pocitat, zavedu si substituci  , takze resim, kdy plati
, takze resim, kdy plati 
Aby nerovnice platila, musi vyraz v absolutni hodnote davat vysledky od 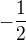 do
do  vcetne techto bodu. Pro nalezeni techto krajnich bodu vyresim rovnice:
vcetne techto bodu. Pro nalezeni techto krajnich bodu vyresim rovnice:
a)  (levy okraj cervene krivky na jednotkove kruznici)
(levy okraj cervene krivky na jednotkove kruznici)
b)  (pravy okraj cervene krivky na jednotkove kruznici)
(pravy okraj cervene krivky na jednotkove kruznici)
Takze ad a) z jednotkove kruznice vyplyva, ze  . Prestoze hledame reseni jen na intervalu
. Prestoze hledame reseni jen na intervalu  , pro jistotu prictu periodu
, pro jistotu prictu periodu  kde k je z mnoziny celych cisel.
kde k je z mnoziny celych cisel. , vratim se k puvodni promenne.
, vratim se k puvodni promenne. nasobim 2
nasobim 2 ,
,
v intervalu, na kterem hledame reseni, ale lezi jen  .
.
Podobne ad b) z jednotkove kruznice vyplyva, ze  . Zase bych mela pro jistotu pricist periodu
. Zase bych mela pro jistotu pricist periodu  , ale dopadlo by to jako ad a), takze to ted vynecham ;-). Vratim se k puvodni promenne
, ale dopadlo by to jako ad a), takze to ted vynecham ;-). Vratim se k puvodni promenne
 nasobim 2
nasobim 2 .
.
Resenim na  jsou vsechna x z intervalu
jsou vsechna x z intervalu 
Pokud davas prednost grafu, je to na obrazku vpravo. Nacrtla jsem si postupne na intervalu <0, 2*pi> fce
y = cos x (teckovane)
y = cos 2x (carkovane), jde o polovinu predchozi fce dvojnasobne "roztazenou" v ose x
y = |cos 2x| (plne cerne), cast predchozi fce, ktera byla pod osou x je zrcadlove prekreslena nad osu x
Vyznacila jsem vodorovnou carou i hodnotu y = 1/2 a na grafu fce y = |cos 2x| (zobrazene plne cerne) hledame jen body, ktere lezi na teto primce y = 1/2 a nebo jsou pod ni (zvyrazneno modre). Krajni body teto vyznacene casti by se stejne museli urcit bud z puvodniho grafu y = cos x, ja uz je popsala podle sveho predchoziho vypoctu.
No tak jsem zvedava, zda je tohle podle tebou ocekavaneho vysledku.
Offline
#8 08. 05. 2008 15:08
- petulkacip
- Příspěvky: 38
- Reputace: 0
Re: goniometrie
↑ Jorica: DEKUJU MOC, uzasneeeee!!!!!!!!
Offline


