Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 01. 2011 15:14
kombinatorika..
Zdravim, mohl by mi nekdo pomoct s timhle prikladem?
Mame partu 11 devcat, 12 kluku a jednoho ucitele. Pro osum z nich prijeli taxiky (po styrech v kazdem), zbytek vali tramvaji. Kolika zpusoby to de udelat, a vime, ze v jednom taxiku byli jenom holky a v dalsim byli jenom kluci. Ucitel muze jit cim chce ba i tramvaji.
Muze to byt C(11,4)xC(12,4)?
a co mam udelat s tym zbytkem? Treba + 16?
Dekuji za radu.
Offline
#2 18. 01. 2011 16:32
Re: kombinatorika..
Výpočet rozdělíme na tři disjukntní části podle toho, čím pojede učitel.
1) Uvedený výpočet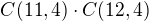 
správně jen když učitel jede tramvají.
2) Pokud ale pojede taxíkem s klukama, tak celkový počet takových možností je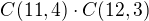 
, protože v druhém taxíku jsou už jen 3 místa.
3) doplníte sám....
Hledaný počet řešení je součtem počtu uvedených možností, neboť žádná jistě není započítána dvakrát a na nic jsme nezapomněli.
Co jste myslel tím "zbytkem"?
Odkud se vzalo číslo 16?!?
Offline
#3 18. 01. 2011 17:20
Re: kombinatorika..
↑ petrkovar: spatne jsem nad tim uvazoval ani sam nevim kde jsem to vzal..takze vysledny pocet je jen souctem danych dvou moznosti?
Offline
#5 18. 01. 2011 21:42
Re: kombinatorika..
↑ petrkovar: napada me jen jedna moznost : ucitel nepujde ani tramvaji ani taxikem : C(11,4) X C(12,4) je to spravne?
Offline
#6 19. 01. 2011 21:24
Re: kombinatorika..
↑ DiPietro:Ne, není. Třetí možnost je, že pojede s děvčaty. Protože učitel může jet čím chce.
Offline