Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Prosba o pomoc řešení příkladů ke zkoušce z kombinatorických metod
#2 20. 01. 2011 17:37
Re: Prosba o pomoc řešení příkladů ke zkoušce z kombinatorických metod
Jedná se o učebnicové příklady a nemyslím si, že patří mezi "zajímavé". Proto jsem téma přesunul.
Nápovědy:
2) začal bych obrázkem, pak úlohu půjde rozdělit na několik podúloh a výsledek dostaneme sečtením jednotlivých výsledků
3) s výhodou využijeme derivaci funkce, určitě máte podobný příklad v učebním textu
4) brali jste Kirchhoffovu větu?
Offline
#3 20. 01. 2011 17:43
Re: Prosba o pomoc řešení příkladů ke zkoušce z kombinatorických metod
↑ petrkovar:
Omlouvám za zařazení do špatné kategorie.
2. neměli.
3. nebrali.
Offline
#4 20. 01. 2011 17:58
Re: Prosba o pomoc řešení příkladů ke zkoušce z kombinatorických metod
↑ pitrsonek:A jaký učební text máte k dispozici?
Offline
#6 20. 01. 2011 19:33
Re: Prosba o pomoc řešení příkladů ke zkoušce z kombinatorických metod
↑ petrkovar:
Skripta:
http://risk.rss.tul.cz/Members/RaD/publ … DIM_II.pdf
děkuji za tip
2. příklad už tuším jak na to:
Dobrá myšlenka je si označit posun bodu vlevo jako 0 a posun vpravo jako 1
Z bodu Start [x1,y] se musite dostat do bodu END [x2,y2]
p0 = x1 - x2
p1 = y1 - y2
p0 a p0 udávají počet potřebných znaků (0,1), které jsou nutné pro realizaci cesty do bodu.
Celkový počet cest jen permutace s opakováním, P(p0, p1), aby řešení odpovídalo zadání je nutné vyloučit cesty, které obsahují zakázané úseky.
Offline
#7 20. 01. 2011 20:30
Re: Prosba o pomoc řešení příkladů ke zkoušce z kombinatorických metod
K příkladu 4). Bude dobré si graf nakreslit a uvědomit si, kolik hran má zůstat a také že z jistých dvojic hran musí vždy alespoň jedna zůstat.
Offline
Stránky: 1
- Hlavní strana
- » Projekty a příklady z Diskrétní matematiky
- » Prosba o pomoc řešení příkladů ke zkoušce z kombinatorických metod


 vytvořující funkcí posloupnosti
vytvořující funkcí posloupnosti 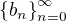 tak
tak  je vytvořující funkcí posloupností
je vytvořující funkcí posloupností  .
.