Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nulová derivace implikuje konstantnost (TOTO TÉMA JE VYŘEŠENÉ)
#1 18. 01. 2011 15:54
Nulová derivace implikuje konstantnost
Zdravím,
pokouším se připravovat na zkoušku z matematické analýzy. Četl jsem si, co se dělalo na přednášce, a strašně se mi nedařilo dokázat následující tvrzeníčko:
Buď 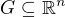 otevřená souvislá a
otevřená souvislá a 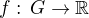 zobrazení takové, že
zobrazení takové, že 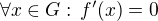 . Pak je
. Pak je  konstantní na G.
konstantní na G.
Bohužel si moc nepamatuji, jak se toto dokazovalo na přednášce, ovšem napadl mne trochu jiný důkaz, trochu kuriózní. Prosím o kontrolu:
Nejprve ukážeme, že  je Darbouxovská. Kdyby totiž bylo
je Darbouxovská. Kdyby totiž bylo  pro nějaká
pro nějaká  a zároveň
a zároveň 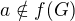 , tak
, tak 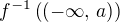 a
a 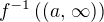 tvoří disjunktní pokrytí
tvoří disjunktní pokrytí  dvěma otevřenými neprázdnými množinami - spor.
dvěma otevřenými neprázdnými množinami - spor.
Snadno se (z nějaké věty o střední hodnotě nebo něčeho takového) ukáže, že v každé kouli 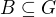 musí být z podmínky
musí být z podmínky  funkce konstantní. Jenže
funkce konstantní. Jenže  má spočetnou bázi z koulí, tím pádem lze
má spočetnou bázi z koulí, tím pádem lze  napsat jako spočetné sjednocení koulí. V každé této kouli je
napsat jako spočetné sjednocení koulí. V každé této kouli je  konstantní, tím pádem může
konstantní, tím pádem může  na
na  nabývat pouze spočetně mnoha hodnot. Ovšem darbouxovskost vynucuje, že funkce
nabývat pouze spočetně mnoha hodnot. Ovšem darbouxovskost vynucuje, že funkce  už nabývá
už nabývá 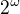 hodnot, pokud nabývá nějakých dvou hodnot - spor.
hodnot, pokud nabývá nějakých dvou hodnot - spor.
Offline
- (téma jako vyřešené označil(a) Olin)
#2 18. 01. 2011 17:25
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Nulová derivace implikuje konstantnost
A nešlo by aplikovat přímo větu o střední hodnotě? (f(a)-f(b))/(a-b)=f'(x) pro nějaké x mezi a,b (tím pro f(a)<>f(b) dostaneme f'(x)<>0 a spor.). a,b,x může být i-tá souřadnice příslušného bodu v prostoru Rn. (Tj. z vektoru (v1,..,vn) zkoumáme jen složku vi.) Taková i-tá souřadnice jistě bude existovat, pokud f(A)<>f(B) (zde A,B jsou už z Rn).
"Máte úhel beta." "No to nemám."
Offline
#3 18. 01. 2011 17:37
Re: Nulová derivace implikuje konstantnost
Vůbec nechápu. Děláš větu o střední hodnotě nějak po složkách a pak z toho vyvozuješ něco pro střední hodnotu mezi body v prostoru?
Offline
#4 18. 01. 2011 21:23
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Nulová derivace implikuje konstantnost
Použiju jen větu o střední hodnotě pro jednu nezávisle proměnnou (z R1).
Postup:
1) Pro spor nechť f(A)<>f(B). Pak existují odpovídající složky a,b vektorů A,B, že a<>b. Nechť jsou to složky s indexem "i".
2) Uvažujme body Y úsečky A-B, resp. jejich i-tou souřadnici y. Každému takovému bodu odpovídá hodnota f(Y) (označme ji f(y)). Tj. jsme náš problém převedli do řeči funkce jedné proměnné. Použijeme větu o střední hodnotě - existuje x, že f'(x)=(f(b)-f(a))/(b-a). Je tedy f'(x)<>0.
3) Z f'(x)<>0 plyne f'(X)<>0 (X je z Rn a leží na úsečce A-B), což je onen spor.
(Krok 3 je nutné dokázat formálněji.)
"Máte úhel beta." "No to nemám."
Offline
#5 19. 01. 2011 11:37
Re: Nulová derivace implikuje konstantnost
↑ check_drummer:
Obávám se, že tvůj postup vyžaduje, aby vyšetřovaná množina byla konvexní, jelikož spojuješ body A a B úsečkou.
Jinak již jsem z kolegových zápisků odhalil původní řešení: vzor jednobodové množiny v zobrazení f je určitě uzavřená množina, ovšem je taky otevřená (právě díky tomu, že v kouli musí být díky nulovosti derivace funkce konstantní a G je otevřená), ovšem jediné obojetná množiny v souvislé množině jsou prázdná nebo celá množina.
Offline
#6 19. 01. 2011 20:22
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: Nulová derivace implikuje konstantnost
↑ Olin:
Pravda, nevšiml jsem si podmínky na G.
Tak jinak (a pravda volněji, možná jsem nechal nějaké slabé místo): zvolme cestu mezi A a B, která je dána souvislostí - nechť je parametrizována spojitou funckcí s(t), že s(0)=A,s(1)=B. Označme k=inf{t, f(s(t))<>f(A)}. Pak ale díky tomu, že (jak jsem psal minule pro konvexní množiny) na každém okolí B každého bodu, které leží v G, je f konstantní, bychom pro k>0 dostali spor (buď volbou k', kde s "opouští" toto okolí B, nebo případně pokud je s(0) přímo v tomto okolí). Pro k=0 zase dostaneme spor s tím, že f je v nějakém okolí s(0) konstantní.
"Máte úhel beta." "No to nemám."
Offline
#7 20. 01. 2011 11:11
Re: Nulová derivace implikuje konstantnost
↑ check_drummer:
To už zní lépe, jen mám pocit, že to vyžaduje dokonce obloukovou souvislost (existence "cesty").
Offline
#8 20. 01. 2011 14:00
Re: Nulová derivace implikuje konstantnost
↑ Olin:
Připadá mi, že Tvůj důkaz je v pořádku, navíc docela elegantní.
↑ Olin:
Je "oblouková" souvislost otevřené množiny G v R^n (totiž že libovolné dva navzájem různé body mn. G lze "spojit" lomenou čarou ležící v G)
něco silnějšího než obecná souvislost definovaná topologicky (prostor G je souvislý, právě když ho nelze vyjádřit jako disjunktní sjednocení
dvou svých neprázdných otevřených částí) ? Domnívám se, že ne.
Offline
#9 20. 01. 2011 14:12
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nulová derivace implikuje konstantnost
↑ Rumburak:
Myslím, že oblouková souvislost je silnější než jen souvislost, na wikipedii je i příklad.
Offline
#10 20. 01. 2011 14:20
Re: Nulová derivace implikuje konstantnost
↑ Rumburak: ↑ BrozekP:
Já mám poslední dobou pocit, že otevřená souvislá množina už by mohla být obloukově souvislá. Tedy, nikde jsem to nečetl ani neslyšel, pořádný důkaz ještě nemám, ale když si to představím, tak by to platit mohlo. Víte o tom někdo něco?
Offline
#11 20. 01. 2011 14:39
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nulová derivace implikuje konstantnost
Offline
#12 20. 01. 2011 14:54
Re: Nulová derivace implikuje konstantnost
↑ BrozekP:
Jistě, to asi funguje. Zkusím to tedy upřesnit: existuje otevřená souvislá množina v  , která není obloukově souvislá?
, která není obloukově souvislá?
Offline
#13 20. 01. 2011 14:54
Re: Nulová derivace implikuje konstantnost
↑ BrozekP: není, protože ta množina není otevřená. na komplexce jsme dokazovali, že pro otevřenou 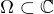 je souvislost a oblouková souvislost ekvivalentní. v
je souvislost a oblouková souvislost ekvivalentní. v  to myslím je analogický
to myslím je analogický
Offline
#14 20. 01. 2011 14:57
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Nulová derivace implikuje konstantnost
Offline
#15 20. 01. 2011 16:15 — Editoval Rumburak (20. 01. 2011 16:32)
Re: Nulová derivace implikuje konstantnost
↑ BrozekP: , ↑ Olin:
Je-li A graf funkce sin (1/x) a B uzávěr této množiny v R^2 (operace uzávěru přidá k množině A úsečku s krajními body [0,-1], [0,1]),
pak B je souvislá a nikoliv obloukově, to je pravda. Množina B je neprázdná uzavřená v R^2 a nemůže být zároveň otevřená v R^2,
to by pak prostor R^2 nebyl souvislý.
(B je samozřejmě otevřená a zároveň i uzavřená sama v sobě, což je triviální vlastnost každého topologického podprostoru).
Pokusím se dokázat, že otevřená souvislá množina v 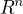 je obloukově (=křivkově) souvislá.
je obloukově (=křivkově) souvislá.
Mějme neprázdnou množinu  otevřenou v
otevřenou v 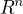 , která je navíc souvislá (případ prázdné pnožiny je triviální).
, která je navíc souvislá (případ prázdné pnožiny je triviální).
Pro 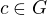 položme
položme
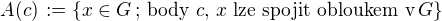 .
.
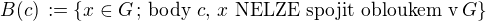 .
.
Využijeme-li předpokladu o otevřenosti a neprázdnosti množiny  a faktu, že koule je obloukově souvislá, pak snadno nahlédneme,
a faktu, že koule je obloukově souvislá, pak snadno nahlédneme,
že množina 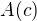 je otevřená v
je otevřená v 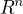 i v
i v  , navíc neprázdná.
, navíc neprázdná.
Jestliže 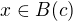 , pak pro každou otevřenou kouli
, pak pro každou otevřenou kouli 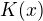 (x je střed) ležící v
(x je střed) ležící v  zároveň platí, že
zároveň platí, že 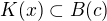 , jinak bychom
, jinak bychom
prostřednicvím vhodného bodu 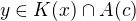 snado sestrojili oblouk z
snado sestrojili oblouk z  do
do  v
v  (opět zde využíváme obloukovou souvislost koule).
(opět zde využíváme obloukovou souvislost koule).
Tedy rovněž 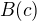 je otevřená v
je otevřená v 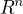 i v
i v  .
.
Předpokládejme, že množina  není obloukově souvislá. Potom existují body
není obloukově souvislá. Potom existují body 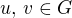 , které nelze spojit obloukem v
, které nelze spojit obloukem v  .
.
Tedy 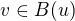 . Potom ale
. Potom ale 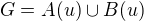 , kde
, kde 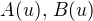 jsou neprázdné otevřené v
jsou neprázdné otevřené v  ,
, 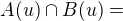 .
.
To je ovšem ve sporu s předpokladem o souvislosti množiny  .
.
Souvislá otevřená množina v 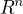 je tedy obloukově souvislá. Obrácená implikace je, myslím, celkem snadná.
je tedy obloukově souvislá. Obrácená implikace je, myslím, celkem snadná.
EDIT. Za tu dobu, co jsem to vyťukával (včetně vymýšlení) je to již, jak vidím, jasné. Nicméně důkaz už tu nechám, třeba jen proto,
aby v něm někdo případně našel chybu :-) .
Offline
#16 20. 01. 2011 22:43
Re: Nulová derivace implikuje konstantnost
↑ BrozekP:
V pořádku, já svůj výrok původně myslel o obecném metrickém prostoru, díky za vyvedení z omylu. Právě jsem se příliš soustředil na to  .
.
↑ Rumburak:
Díky, myslím, že ten důkaz je zcela v pořádku.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Nulová derivace implikuje konstantnost (TOTO TÉMA JE VYŘEŠENÉ)