Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Prubeh funkce - opet (TOTO TÉMA JE VYŘEŠENÉ)
#1 11. 05. 2008 11:56
Prubeh funkce - opet
Ahoj potrebovala bych pomoct s prubehem fce
Definicni obor mi vysel od -1 do +1
Neni periodicka, suda ani licha, to je asi jasne. Snad:)
Prvni derivace mi vysla uz docela divne, nevim jestli je dobre, ale snad jo...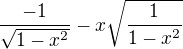
Tak a ted urcit ty nulove body, to uz si nevim rady:( Diky za vasi pomoc
Offline
#5 11. 05. 2008 13:57
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Prubeh funkce - opet
leniczka napsal(a):
Diky, super. Takze nulovy bod je -1. ze?
ne, pro x=-1 derivace neexistuje
Offline
#6 11. 05. 2008 14:01
Re: Prubeh funkce - opet
Díky. No je to zřejmé, že ta fce je klesající. Jen nevím, jak to dokázat a zapsat. Jsem zvyklá, že když vyšetřuju průběh fce, tak je D=R a taky že ty nulové body jsou dva. Tady je jen jeden -1 a jsem z toho nějaká zmatená:) Nešel by nějak nastínit další postup? Díky
Offline
#8 11. 05. 2008 14:31 — Editoval robert.marik (11. 05. 2008 14:32)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Prubeh funkce - opet
↑ leniczka:
koukal jsem na to blíž. do té derivace nejde dosadit x=-1, protože vyjde nula ve jmenovateli.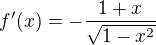
Ale dá se spočíat, k čemu se ta derivace blíží (0), nebo se to dá upravit na 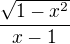 , takže ta nula vlastně skutečně je stacionárním bodem. Omlouvam se. Psal jsem to v rychlosti.
, takže ta nula vlastně skutečně je stacionárním bodem. Omlouvam se. Psal jsem to v rychlosti.
funkce na intervalu [-1,1] klesá, v x=-1 má vodorovnou tečnu, v x=1 svislou, druhá derivace je taky všude záporná, bude to tedy jenom takový klesající konkávní oblouček z bodu x=-1, y=pi do bodu x=1, y=0
http://wood.mendelu.cz/math/maw/prubeh/ … ko=Odeslat
Offline
#9 11. 05. 2008 15:22
Re: Prubeh funkce - opet
↑ robert.marik:
Už to skoro mám:) Ještě nějaké dotazy. Druhá derivace je všude záporná, to je jasné, dosadím si pár bodů a jde to vidět. Ale jak to mám normálně dokázat? Když to dokážu, tak co jsem vlastně tou druhou derivací zjistil a jaký to má vliv na ten graf? A všude píšou, že se mají určit i limity. Na co tam jsou v mém případě? Díky za odpověd
Offline
#10 11. 05. 2008 16:04
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Prubeh funkce - opet
druhá drivace nemá na intervalu (-1,1) ani nulové body, ani bod nespojitosti. Podle 1. Bolzanovy věty tam nemůže být změna znaménka. Totéž platí i pro první derivaci.
Offline
#11 11. 05. 2008 17:31
Re: Prubeh funkce - opet
↑ robert.marik:
Takže mám jen vypočíst druhou derivaci...ale co mám k tomu napsat?? A mám počítat limity? Jak zjistím jestli je konkávní nebo konvexní? děkuji:)
Offline
#12 11. 05. 2008 18:07
Re: Prubeh funkce - opet
Podle mě je v případě takovéhoto definičního oboru zbytečné počítat nějaké limity, ani mě nenapadá jaké.
Konkávnost a konvexnost zjistím podle toho, jaké znaménko má druhá derivace, viz např. http://cs.wikipedia.org/wiki/Konvexnost … ost_funkce
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Prubeh funkce - opet (TOTO TÉMA JE VYŘEŠENÉ)