#1 11. 05. 2008 19:55
Limita funkce
Zdravím,
prosil bych o pomoc s jednou (pro mě zapeklitou) limitkou... Zkoušel jsem to už počítat přes vytknutí "x" zpod odmocnin, poté dle A-B = (A^3 - B^3) / (A^2 + AB + B^2), a nakonec ještě pokus přes rozšíření, nejdříve 3odm(x+1) + 3odm(x-1) / 3odm(x+1) + 3odm(x-1) a jelikož nešlo, tak poté i standartním 3odm((x+1)^2) + 3odm((x-1)^2) / 3odm((x+1)^2) + 3odm((x-1)^2) ... A? jsem počítal jak jsem počítal, vždy jsem se dostal k neurčitým výrazům, povětšinou tedy zakomponovaného oo - oo :(
Budu rád za jakýkoliv "nákop"...
Offline
? pak by vyslo 
, jestli sem nekde neudelal chybu, teda.#5 11. 05. 2008 21:33
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Limita funkce
a nemá to být náhodou ![$\sqrt[3]{(x+1)^4} + \sqrt[3]{(x+1)^2(x-1)^2} + \sqrt[3]{(x-1)^4}$](/mathtex/ca/caf34c75897066e5efc05417ff7f9bec.gif "kopírovat do textarea")
?
Aby vyšlo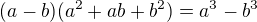 
nějak v prispevku #2 nevidím, kam zmizely ty odmocniny :(
Offline
#6 11. 05. 2008 21:36 — Editoval robert.marik (11. 05. 2008 21:39)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Limita funkce
santic napsal(a):
poté dle A-B = (A^3 - B^3) / (A^2 + AB + B^2), a
tohle nepomoho? Mělo by. Uvnitř té limity potom bude![$\frac{(x+1)^2-(x-1)^2}{\sqrt[3]{(x+1)^4} + \sqrt[3]{(x+1)^2(x-1)^2} + \sqrt[3]{(x-1)^4}}= \frac{4x}{\sqrt[3]{(x+1)^4} + \sqrt[3]{(x+1)^2(x-1)^2} + \sqrt[3]{(x-1)^4}} $](/mathtex/af/af8688b4f4dab9ba7314ff9947dbbb01.gif "kopírovat do textarea")
ve jmenovateli vytknu x^(4/3), to co zbude v zavorce konverguje k nejake konstante a po castecnem zkraceni x s citatelem zustane v citateli konstanta a jmenovatel pujde do nekonecna. limita tedy bude nula.
Offline