Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vyšetření monotomie. (TOTO TÉMA JE VYŘEŠENÉ)
#2 25. 01. 2011 16:28
Re: Vyšetření monotomie.
Přepočítej si tu derivaci funkce f . Mně vyšlo
Offline
#3 25. 01. 2011 16:36
Re: Vyšetření monotomie.
↑ Rumburak:
Derivaci mám správně http://www.wolframalpha.com/input/?i=%2 … 284-x^2%29
Offline
#6 25. 01. 2011 17:46
Re: Vyšetření monotomie.
↑ da.backer:
ALe když dosadím abych zjistil kde je kles. atp. tak mi to pořád vychází jinak než ve výsledku.
Offline
#7 25. 01. 2011 19:50 — Editoval Tychi (25. 01. 2011 19:59)
Re: Vyšetření monotomie.
vždyť máš tu derivaci jinak než wolfram, lišíš se znaménkem
a..jedná se o monotonii ne monotomii
Ještě mě napadá..
dost chaotický je ten zápis, nebo spíš špatný
z nerovnice 
přece plyne, že absolutní hodnota x je menší než 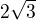 , čili
, čili  a zároveň
a zároveň  ,
,
čili funkce je rostoucí na intervalu 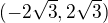
Vesmír má čas.
Offline
#8 25. 01. 2011 20:07 — Editoval da.backer (25. 01. 2011 20:11)
Re: Vyšetření monotomie.
No derivace je správě, jenom každá jinak upravená ;)
To je právě to co si nedokáži představit
Tychi napsal(a):
z nerovnice
přece plyne, že absolutní hodnota x je menší než, čili
a zároveň
,
čili funkce je rostoucí na intervalu
Proto jsem to začal řešit jinak a to že nedávám <a > ale pouze =.
Jěště si to zkusim přepsat a spočítat ;) Děkuji.
Offline
#10 25. 01. 2011 22:12 — Editoval Tychi (25. 01. 2011 22:15)
Re: Vyšetření monotomie.
uf, cos to provedl s tím jmenovatelem?(o:
jmenovatel je druhá mocnina čehosi, takže stále kladný.. (to umocnění cos provedl je velký úlet)
dosazení do jmenovatele provádíš taky špatně, přece např 
a v té původní derivaci vidím mínus ve jmenovateli, což z toho dělá jiný zlomek..
Vesmír má čas.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vyšetření monotomie. (TOTO TÉMA JE VYŘEŠENÉ)

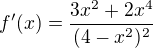 .
. 

