Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Derivace v bodě (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 01. 2011 20:40
Derivace v bodě
Něco pro odpočinek:
Dokažte nebo vyvraťte tvrzení
Je-li reálná funkce f definovaná v okolí v bodu  a má v něm derivaci, pak platí
a má v něm derivaci, pak platí 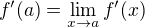 .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
- (téma jako vyřešené označil(a) BrozekP)
#2 25. 01. 2011 23:22
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Derivace v bodě
Offline
#3 26. 01. 2011 07:08
Re: Derivace v bodě
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 26. 01. 2011 10:01
Re: Derivace v bodě
pokud si to správně pamatuju,
Offline
#5 26. 01. 2011 10:42
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Derivace v bodě
Offline
#6 26. 01. 2011 15:23 — Editoval Pavel (26. 01. 2011 15:25)
Re: Derivace v bodě
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#7 28. 01. 2011 00:41
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Derivace v bodě
Označil jsem téma jako nevyřešené, pojďme prosím ještě rozhodnout o pravdivosti následujícího tvrzení:
Je-li reálná funkce f definovaná v okolí v bodu  , má na tomto okolí derivaci a existuje vlastní limita
, má na tomto okolí derivaci a existuje vlastní limita 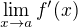 , pak platí
, pak platí 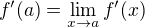 .
.
Offline
#8 28. 01. 2011 13:40
Re: Derivace v bodě
↑ BrozekP: nerad se opakuju, ale nenapsal, jsi, že ta derivace má být vlastní...
Offline
#9 28. 01. 2011 14:18
Re: Derivace v bodě
Offline
#10 28. 01. 2011 15:04
Re: Derivace v bodě
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#11 28. 01. 2011 16:47
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Derivace v bodě (TOTO TÉMA JE VYŘEŠENÉ)
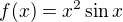 pro
pro 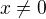 a
a  .
. 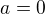 .
.

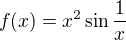

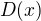 je Dirichletova funkce.
je Dirichletova funkce.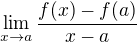 .
.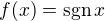 v bodě
v bodě