Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 28. 01. 2011 17:17

RUFFRIDE
Příspěvky: 69
Reputace:   12 
 

dokaz delitelnosti matematickou indukciou

zdravim, potreboval by som poradit s dokazom 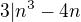$3|n^3-4n$
upravil som na sucin 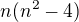$n(n^2-4)$
skusim pre n=1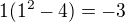
$1(1^2-4)=-3$ je delitelne 3
plati pre k, skusim k+1
$(k+1)\((k+1)^2-4\)=(k+1)(k^2+2k+1-4)=(k+1)(k^2+2k-3)=k^3+2k^2-3k+k^2+2k-3=k^3+3k^2-k-3$
mam to potial dobre? co z toho vyplyva?
dakujem za nejaku pomoc

Offline

  • (téma jako vyřešené označil(a) BakyX)

#2 28. 01. 2011 17:21

jarrro
Příspěvky: 5472
Škola: UMB BB Matematická analýza
Reputace:   303 
Web
 

Re: dokaz delitelnosti matematickou indukciou

↑ RUFFRIDE:áno je to dobre to posledné sa ešte dá upraviť na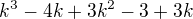
$k^3-4k+3k^2-3+3k$z čoho už pravdivosť dokazovaného tvrdenia vyplýva

MATH IS THE BEST!!!

Offline

 

#3 28. 01. 2011 17:24 — Editoval RUFFRIDE (28. 01. 2011 17:25)

RUFFRIDE
Příspěvky: 69
Reputace:   12 
 

Re: dokaz delitelnosti matematickou indukciou

aha , chapem odcitali sme -3k a pripocitali spat, ale podla coho viem ze je to hotovo, dokazane?

Offline

 

#4 28. 01. 2011 18:17

BakyX
Cat Lover & S.O.A.D. Lover
Příspěvky: 3416
Škola: UPJŠ
Pozice: Študent
Reputace:   158 
 

Re: dokaz delitelnosti matematickou indukciou

Ahoj.. ;)

Máš dokázať teraz toto:

$3|k^3+3k^2-k-3$

Zrejme platí:

$3|3k^2\nl 3|-3$

Môžeš preto upraviť horné tvrdenie na: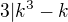

$3|k^3-k$

A toto upravuješ:

$3|k(k^2-1)\nl 3|k(k+1)(k-1)$

Toto je vždy deliteľné 3. Chápeš prečo ?

1^6 - 2^6 + 3^6 = 666

Offline

 

#5 28. 01. 2011 18:50

RUFFRIDE
Příspěvky: 69
Reputace:   12 
 

Re: dokaz delitelnosti matematickou indukciou

dakujem, chapem su to 3 posebe iduce cisla jedno znich je urcite delitelne 3 ;)

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson