Matematické Fórum

O.o · 14. 05. 2008 16:39 — Editoval O.o (14. 05. 2008 16:51)

Ahoj,
potřeboval bych od někoho prosím nutně pomoci. Nějak nemohu hnout s jedním (určitě jednoduchým příkladem). Byl bych vděčný, kdyby mi mohl někdo pomoci.

Př:
Určete definiční obor dané funkce a zda je funkce lichá, sudá nebo periodická:

f(x) = log(cos x) + log(sin x)

K tomu definičnímu oboru mne napadlo, že bych řešil výrazy logaritmů jako větší než nula.
$cos x > 0 \wedge sin x > 0$
(I, IV) (I, II)
Společný kvadrant je I, takže jsem určil deifiniční obor takto: $x\in(0;90)$ - stupně.
S tou periodičností jsem si nebyl jistý. Ve škole nám říkali, že periodické funkce jsou pro nás pouze goniometrické, jiné periodické, že nás učit nebodou (není to v osnovách), ale nevím jak to tady zkloubit s těmi logaritmi.

Nemohl by jste mi někdo, prosím, poradit, jestli je to takto správně a jak pokračovat dál (určení zda je funkce lichá, sudá nebo periodická)?

Děkuji všem za případnou pomoc..

Olin · 14. 05. 2008 16:55

S tím prvním kvadrantem máš pravdu, jenže musíš i při výpočtu toho def. oboru započítat to, že jsou sinus a kosinus periodické. Správný zápis by asi měl být

$D(f) = \bigcup_{k \in \mathbb{Z}} \left ( 2k\pi;\, \frac{\pi}{2} + 2k\pi \right )$

což sice asi vypadá dost děsivě, ale znamená to asi tolik, že máme ten základní interval 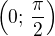$\left ( 0;\, \frac{\pi}{2} \right )$ , který můžeme libovolně posouvat o $2\pi$ oběma směry, protože sinus i kosinus mají periodu $2\pi$ .

Co se týče periodičnosti, všimni si, že x je všude jako argument goniometrických funkcí, takže když k němu přičteme libovolný násobek $2\pi$ , argument logaritmu se nezmění. Platí tedy
$\forall k \in \mathbb{Z}:\, f(x) = f(x + 2k\pi)$

Funkce je tedy periodická s periodou $2\pi$ .

A ještě k paritě funkce - obvykle se to dělá přes dosazení -x do argumentu, ale tady se stačí podívat na ten definiční obor a hned vidíme…

O.o · 14. 05. 2008 17:05

Děkuji moc.
S tou sudou/lichou funkcí jsem si zkoušel po odeslání dotazu dosadit -x (sudá funkce) a pak -f(x). Nevyšlo mi ani jedno, takže asi zůstanu u periodičnosti.

Ještě jednou díky ;)

Matematické Fórum

#1 14. 05. 2008 16:39 — Editoval O.o (14. 05. 2008 16:51)

Funkce - logaritmická

#2 14. 05. 2008 16:55

Re: Funkce - logaritmická

#3 14. 05. 2008 17:05

Re: Funkce - logaritmická

Zápatí