Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 01. 2011 20:50
priklad
Na určovanie vzdialenosti rôznych objektov sa využívajú rádiolokátory (radary).
Radar je zariadenie, ktoré vysiela elektromagnetické vlny a následne sníma ich
odraz od objektu, ktorý je schopný ich odrážať. Impulzný rádiolokátor na
regionálnom letisku vysiela 5000 impulzov za sekundu pričom doba trvania jedného
impulzu je 18 ns. Radarom vysielané vlny majú vlnovú dĺžku 14 cm.
a) Koľko elektromagnetických kmitov obsahuje jeden impulz vyslaný radarom?
b) Aký je dosah radaru, t.j. v akej najväčšej vzdialenosti od letiska dokáže radar
zachytiť sledované objekty?
vobec si s tym neveim rady tak ak by sa nasiel niekto kto by mi vedel poradit bola by som velmi vdacna:)
Offline
- (téma jako vyřešené označil(a) medvidek)
#2 31. 01. 2011 04:17
Re: priklad
↑ miskaaa:
a) počet kmitov:
Vlnová dĺžka radarového žiarenia 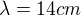 .
.
Perióda elektromagnetického vlnenia 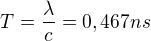 .
.
Doba trvania radarového impulzu 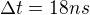 .
.
Koľko kmitov o perióde  je treba na pokrytie časového úseku
je treba na pokrytie časového úseku  ?
?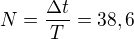
a) to isté trochu inak:
Doba trvania radarového impulzu 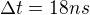 .
.
Radarové žiarenie za túto dobu prekoná vzdialenosť 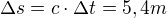 .
.
Koľko vlnových dĺžok 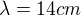 je treba na pokrytie tejto vzdialenosti?
je treba na pokrytie tejto vzdialenosti?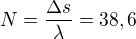
b) dosah:
Tu budem len hádať.
Predpokladám, že odrazený signál sa musí do radaru vrátiť skôr, než je vyslaný ďalší signál.
Na cestu tam a späť máme čas 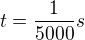 .
.
Z toho vyplýva maximálna vzdialenosť objektu 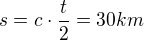 .
.
Offline