Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 02. 2011 12:21
Střední hodnota a odchylka
Zdravím,
nevím si moc rady s jednou úlohou, mám k ní sice řešení, ale nevím u rozptylu jak k tomu výsledku dojít
Překlad je snad nějak takhle: Představ si, že N položek je testováno simultánně a že položky mají nezávislé životnosti, všechny exponenciálně distribuovány s parametrem lambda. Najdi střední hodnotu a odchylku délky času až do porouchání R položek
Podle toho výsledku je , že pro R=1, doba do porouchání jedné součástky je rovna 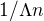 Moje úvaha tedy je, že střední hodnota exp. distribuce je rovna
Moje úvaha tedy je, že střední hodnota exp. distribuce je rovna 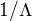 , plus vybírám přesně jednu položku z dohromady N položek, tedy
, plus vybírám přesně jednu položku z dohromady N položek, tedy 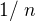 a vynásobím to s tou lambdou
a vynásobím to s tou lambdou
Dál pro R=2, mám N-1 neporouchaných a vybírám z nich opět jednu, která se porouchá, takže 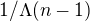
Takhle můžu pokračovat až do R=N a dostanu ten požadovaný výsledek.
Doufám, že by to snad mohlo být dostatečné zdůvodnění do písemky.
S rozptylem si však nevím vůbec rady, vzorec  je jediné co mne k rozptylu napadá, ale to se nedá použít.
je jediné co mne k rozptylu napadá, ale to se nedá použít.
Budu vděčen za jakýkoli nápad, děkuji.
Offline
#2 02. 02. 2011 13:26
Re: Střední hodnota a odchylka
ta tvoje úvaha by asi vyžadovala nějaký zdůvodnění. snadno se spočítá, že minimum z  nezávislých
nezávislých 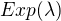 má
má 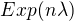 a z bezpaměťovosti exp. rozdělení plyne nezávislost dob mezi jednotlivými selháními, takže stačí střední hodnoty a rozptyly posčítat
a z bezpaměťovosti exp. rozdělení plyne nezávislost dob mezi jednotlivými selháními, takže stačí střední hodnoty a rozptyly posčítat
Offline
