Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Střední škola
- » Soustava lineárních a kvadratických rovnic (TOTO TÉMA JE VYŘEŠENÉ)
#26 02. 02. 2011 18:44
- Dominika84

- Příspěvky: 36
- Reputace: -1
Re: Soustava lineárních a kvadratických rovnic
tak to tedy bude
Y2-10-20=0 ????????? A čím pak tu rovnici teda vykrátím ??????
Offline
#27 02. 02. 2011 18:46
Re: Soustava lineárních a kvadratických rovnic
↑ Dominika84:
Přestaň se furt ptát a zamysli se nad těma jablíčkama. Já vím moc dobře co tam je, a taky vím kolik to vyjde. Až na to přijdeš, zkontroluj si ještě znaménka, taky jsou špatně.
Offline
#28 02. 02. 2011 18:50
- Dominika84

- Příspěvky: 36
- Reputace: -1
Re: Soustava lineárních a kvadratických rovnic
↑ LukasM:
No tak to díky. Já myslela,že na tohle fóru se pomáhá pochopit matika těm co jí nechápou.
Když se pořád ptám,tak to asi znamená že si stím nevím rady a ani nevím jak na to. Tak jak to mám pochopit, když mi řekneš/te ať se furt neptám ??????
Offline
#29 02. 02. 2011 18:54
Re: Soustava lineárních a kvadratických rovnic
↑ Dominika84:
Klidně se ptej, ale nejdřív odpověz na to na co se ptám já.  . Já se ptám kolik se to teda rovná.
. Já se ptám kolik se to teda rovná.
Offline
#30 02. 02. 2011 18:57
- Dominika84

- Příspěvky: 36
- Reputace: -1
Re: Soustava lineárních a kvadratických rovnic
↑ LukasM:
rovná se to nula (podle jablíček)
Offline
#31 02. 02. 2011 19:00 — Editoval miso16211 (02. 02. 2011 19:02)
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Soustava lineárních a kvadratických rovnic










Nie je to ťažké, stačí vyjadriť si jednu neznámu z oboch rovníc a potom riešiť obe vytvorene rovnice.
Poprosil by som o plusku.
Offline
#32 02. 02. 2011 19:05
- Dominika84

- Příspěvky: 36
- Reputace: -1
Re: Soustava lineárních a kvadratických rovnic
↑ miso16211:
děkuji, plusko bylo dáno
Offline
#33 02. 02. 2011 19:09
- Dominika84

- Příspěvky: 36
- Reputace: -1
Re: Soustava lineárních a kvadratických rovnic
↑ Dominika84:
Ale stejně se v tom nějak nechytám. Asi sem natvrdlá....
Mám
X+Y=5
X2-Y2=5
X=5-Y
(5-Y)2 - Y2 =5
25-10Y+Y2-Y2=5
mám to taklhe správně?
Offline
#34 02. 02. 2011 19:10
#35 02. 02. 2011 19:13
- Dominika84

- Příspěvky: 36
- Reputace: -1
Re: Soustava lineárních a kvadratických rovnic
↑ LukasM:
Tak kde sakra dělám chybu ??? :-D
Offline
#36 02. 02. 2011 19:14
- Dominika84

- Příspěvky: 36
- Reputace: -1
Re: Soustava lineárních a kvadratických rovnic
y2 - 10y + 20 = 0
Ano / ne ?
Offline
#37 02. 02. 2011 19:18
Re: Soustava lineárních a kvadratických rovnic
↑ Dominika84:
Chybu děláš pořád u těch jablíček. Jen proto říkám, že bys mohla víc číst a zkoušet než se ptát, není v tom nic zlého. To cos posala v 19:14 už správně není.
Offline
#38 02. 02. 2011 19:20
- Dominika84

- Příspěvky: 36
- Reputace: -1
Re: Soustava lineárních a kvadratických rovnic
↑ LukasM:
Tak já nevím, podle mě když má jedno jabko a někdo mi jej sebere, tak nemám žádný !!!!!!!!!!!!!!!! To znamená NULA
Offline
#39 02. 02. 2011 19:23
Re: Soustava lineárních a kvadratických rovnic
↑ Dominika84:
To je pravda. Ale podle těch tvých rovnic ti to jedno jablko zůstane.
Mám rovnici  . To v té závorce, jak jsi právě napsala, je NULA. Tak proč tam pořád dokola píšeš
. To v té závorce, jak jsi právě napsala, je NULA. Tak proč tam pořád dokola píšeš 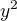 ?
?
Offline
#40 02. 02. 2011 19:28
- Dominika84

- Příspěvky: 36
- Reputace: -1
Re: Soustava lineárních a kvadratických rovnic
↑ LukasM:
Já myslela, že nula se tam nepíše a místo nule se píše y2
Offline
#41 02. 02. 2011 19:32
Re: Soustava lineárních a kvadratických rovnic
↑ Dominika84:
No, a to je právě to místo, kde se ti z žádného jablíčka stane jedno jablíčko. Jablíčko je u nás totiž 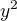 .
.
Nula je nula, a nepíše se místo ní vůbec nic. Pokud ti to není jasné, šel bych o tom diskutovat do sekce ZŠ.
Offline
#42 02. 02. 2011 19:36
- Dominika84

- Příspěvky: 36
- Reputace: -1
Re: Soustava lineárních a kvadratických rovnic
↑ LukasM:
No do sekce ZŠ nevím, nevím........
Dobře tudíž jsme se dopracovaly do fáze 25-10y+0y=5 je to tak
Offline
#43 02. 02. 2011 19:40
Re: Soustava lineárních a kvadratických rovnic
↑ Dominika84:
Ano. S tím, že ti radši pomůžu a rovnou ji přepíšu do tvaru  , abychom se vyhnuli dalším řečem o nule. Teď už by to snad neměl být problém dopočítat.
, abychom se vyhnuli dalším řečem o nule. Teď už by to snad neměl být problém dopočítat.
Offline
#44 02. 02. 2011 19:46
- Dominika84

- Příspěvky: 36
- Reputace: -1
Re: Soustava lineárních a kvadratických rovnic
↑ LukasM:
Tudíž
A=25
B= - 10
C=5
D= B2-4.AC
Je tohle ten postup dál,že?
Offline
#45 02. 02. 2011 19:49 — Editoval mikl3 (02. 02. 2011 19:51)
Re: Soustava lineárních a kvadratických rovnic
↑ Dominika84: pokud je tohle výchozí rovnice, kterou počítáš, tak to není kvadratická, proto nemůžeš použít vzorec pro vypočítání kořenů kvadratické rovnice
pokud je tohle výchozí rovnice, kterou počítáš, tak to není kvadratická, proto nemůžeš použít vzorec pro vypočítání kořenů kvadratické rovnice co třeba odečíst jednu stranu a vyjde něco jako:
co třeba odečíst jednu stranu a vyjde něco jako:  a pak vydělíš rovnici výrazem
a pak vydělíš rovnici výrazem 
nebo takhle: je to příklad lineární rovnice:  (když ji upravíš) a řešení bude
(když ji upravíš) a řešení bude 
Offline
#46 02. 02. 2011 20:34
Re: Soustava lineárních a kvadratických rovnic
↑ Dominika84:
Chybu robíš v tom, že ti chýbajú niektoré absolutné základy matematiky - tj. učivo ZŠ..Máloktorý ôsmak nevie vypočítať  ..Nechcem ťa nijako uraziť, ale tí, ktorí nevedia ZŠ matiku majú na SŠ jednoducho problém..
..Nechcem ťa nijako uraziť, ale tí, ktorí nevedia ZŠ matiku majú na SŠ jednoducho problém..
1^6 - 2^6 + 3^6 = 666
Offline
#47 02. 02. 2011 21:10
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Soustava lineárních a kvadratických rovnic
ideš maturovať z matematiky? diky za plusko
Offline
#48 02. 02. 2011 21:49
Offline
#49 02. 02. 2011 23:03
- Dominika84

- Příspěvky: 36
- Reputace: -1
Re: Soustava lineárních a kvadratických rovnic
↑ miso16211:
Ne nematuruju z matiky, zaplať pánbů :-)
Offline
#50 02. 02. 2011 23:04
- Dominika84

- Příspěvky: 36
- Reputace: -1
Re: Soustava lineárních a kvadratických rovnic
↑ BakyX:
Sorry, ale nepamatuju si, že by se na ZŠ něco takovýho probíralo !!!
Pokud jo, tak mám asi DOOOOST velký výpadek !
Offline
- Hlavní strana
- » Střední škola
- » Soustava lineárních a kvadratických rovnic (TOTO TÉMA JE VYŘEŠENÉ)
