Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 01. 2011 10:37 — Editoval calis (04. 02. 2011 09:43)
Definiční obor (info) 1.1
zdravíčko,
kdy se def obor určuje podle +,- v grafu a kdy podle intervalů ??? je na to nějaké pravidlo ? viz příklad ...(nejsem si jist jak určit D(f))
předem děkuji
Všichni se v něčem předstihujeme, proto se od sebe učíme, je to lidské, nic lidského mi není cizí ... ;)
Offline
- (téma jako vyřešené označil(a) Dana1)
#2 20. 01. 2011 12:21 — Editoval Asqwer (20. 01. 2011 12:28)
Re: Definiční obor (info) 1.1
↑ calis:
u te odmocniny nemuzes napsat, ze citatel je vetsi nebo rovna se 0 a jmenovatel je vetsi nez 0, protoze kdyz citatel je mensi nez 0 a jmenovatel je taky mensi nez 0, tak zlomek je zase vetsi nez 0. Proto musis resit nerovnice (2x-1)/(X+3)>= 0 a melo by ti vyjit, ze x lezi v intervalu (-oo,-3) a <1/2,oo).
-1<x+3<1 /-3
-4< x< -2 => x lezi v intervalu <-4,-2>
Učený hlupák je větší hlupák než hlupák nevzdělaný.
Offline
#3 20. 01. 2011 12:24 — Editoval Dana1 (20. 01. 2011 12:30)
- Dana1
- Host
Re: Definiční obor (info) 1.1
↑ calis:
Prvá nerovnosť v Tvojom obrázku má mať na pravej strane znamienko +.
Ak by tam ten arcsin(x+3) nebol a Ty by si určoval D(f):
Pod odmocninou musí byť nezáporné číslo. Nás učila matikárka, že podiel je kladný presne vtedy, keď aj súčin, iba treba uvážiť, že menovateľ nesmie byť 0.
Riešim teda nerovnicu (ako radí Jelena a Asqwer) (2x - 1)(x + 3) > nanajvýš rovné 0. Na číselnú os vynesiem čísla -3 a 1/2.
Teraz nasleduje dôležitý krok. Na osi vzniknú 3 časti: po číslo -3, medzi -3 a 1/2 a ešte nad 1/2. Potrebujeme zistiť, v ktorej časti má
(2x - 1)(x + 3) hodnotu kladnú. Stačí vziať akékoľvek číslo z príslušnej časti, dosadiť ho do zátvoriek a je to jasné.
Dosaď napr. čísa -4, 0, 1. Zátvorky podľa toho budú mať kladnú hodnotu pre x < -3 alebo aj x > 1/2. (Tu je to Tvoje + z otázky, x je buď z jedného intervalu alebo z druhého, kladné číslo dostaneme aj pre -4, aj pre 1.)
D(f) pre prvú časť príkladu je zjednotenie 2 intervalov, a to x < -3 a x > 1/2. Na osi sa to znázorní šípkou doľava od čísla -3 a šípkou doprava od čísla 1/2. Číslo 1/2 do intervalu patrí (môže vyjsť aj 0), ale číslo -3 nie (menovateľ).
Keďže je tam aj ten arcsin(x+3) a jeho D(f) je interval od -4 do -2 (vrátane -4 aj -2), keby sme zakresľovali jeho D(f), museli by sme spojiť -4 a -2 "mostíkom". Do D(f) patria všetky x medzi -4 a -2, vrátane -4 a -2.
Hodnota celej funkcie sa musí dať vyrátať, preto D(f) tej celej fukcie je PRIENIK oboch definičných oborov, (x musí vyhovovať aj 1. funkcii aj 2., čo je definícia prieniku) .
Mne vyšiel ten prienik interval < -4; -3 ).
#5 03. 02. 2011 22:48
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Definiční obor (info) 1.1
↑ calis:
Zdravím Vás,
pokud je to kompletní řešení umístěné pro řádné uzavření tématu (děkuji :-) potom ještě chybí pro zajištění nezáporné hodnoty pod odmocninou možnost: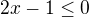 a zároveň
a zároveň  (minus děleno minus dává plus).
(minus děleno minus dává plus).
Překontrolujte to ještě jednou, děkuji.
Offline
#7 04. 02. 2011 13:29
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Definiční obor (info) 1.1
↑ calis:
Nejde o zadání, ale o řešení.
Podíl (+)/(+) je (+),
podíl (-)/(-) je (+).
A přesně takové dvě varianty dosažení kladného čísla pod odmocninou musí být zapsány v řešení.
Ještě výraz pod odmocnou (zlomek) může být nulový, což zajisti nulový čitatel zlomku.
Co na tom, prosím, není jasné? Děkuji.
Offline
#8 04. 02. 2011 13:38
Re: Definiční obor (info) 1.1
↑ jelena: rád bych porozuměl, nechápu.... mám to dobře... jestli mám výsledek špatně , tak napište co je špatně... jinak nemůžu posloužit..., děkuji za pochopení Calis
Všichni se v něčem předstihujeme, proto se od sebe učíme, je to lidské, nic lidského mi není cizí ... ;)
Offline
#9 04. 02. 2011 14:59
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Definiční obor (info) 1.1
↑ calis:
Jen se pokouším uspořádat kroky k nalezení def. oboru zadané funkce.
Zadaní: hledáme def. obor funkce 
Vychozí úvaha: def. obor je interval, kterému náleží x, splňující podmínky: pod znakem 2. odmocniny musí být číslo nezáporné (větší nebo rovné 0) a zároveň argument arcsin musí být v intervalu od -1 do +1.
Cíl: vyřešit soustavu nerovnic: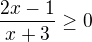
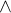

Záleží na Vás, zda cíl bude dosažen. Děkuji a hodně zdaru.
Jelena
Offline
#12 04. 02. 2011 17:10 — Editoval teolog (04. 02. 2011 17:11)
#14 04. 02. 2011 17:17 — Editoval teolog (04. 02. 2011 17:18)
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Definiční obor (info) 1.1
↑ calis:
Oprava -2 na -3 je v pořádku. Ale kde se tam vzalo to od mínus nekonečna? Vždyť to odporuje té druhé podmínce z arcsin!
Navíc Vy hledáte PRŮNIK podmínek vzniklých ze zlomku a z arcsin, protože mají platit zároveň.
Offline
#15 04. 02. 2011 17:19
Re: Definiční obor (info) 1.1
↑ calis: nemůžeš jen opravit výsledek, já myslím ten náčrt, jak máš nad tím, co jsi právě dopsal, ta pluska a mínuska jsou špatně, pro příklad ti ukážu: 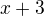
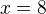
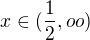
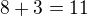 to je kladná hodnota, ty máš, že vyjde vždy záporná (podotýkám skoro všechno takto není dobře jak máš)
to je kladná hodnota, ty máš, že vyjde vždy záporná (podotýkám skoro všechno takto není dobře jak máš)
Offline
#16 04. 02. 2011 17:20
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Definiční obor (info) 1.1
↑ mikl3:
Mně se zdá, že ta minitabulka je celá mimo. Ale původní interval byl dobře, vycházel zřejmě z toho grafického řešení pomocí osy, které bylo v pořádku. Akorát mu tam chybělo to druhé řešení a výsledek podmínky z odmocniny sjednotil z výsledkem z arcsin, což je špatně.
Offline
#19 04. 02. 2011 17:36 — Editoval mikl3 (04. 02. 2011 17:40)
Re: Definiční obor (info) 1.1
↑ teolog: od jedné poloviny do nekonečna má dobře? výraz 2x-1 pro 1 nabývá záporných hodnot? atd....
já myslím jak si namaluje osu vyznačí si nulové body udělá si kolmice na osu s patami na nulových bodech a doleva si napíše ty dva výrazy a do těch intervalů sype + a -, to nemá dobře
4 oblasti nemá dobře
Offline
#20 04. 02. 2011 17:41 — Editoval teolog (04. 02. 2011 17:41)
- teolog


- Místo: Praha
- Příspěvky: 3497
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: Definiční obor (info) 1.1
↑ mikl3:
Ano, ty znaménka jsou mimo. Nechápu, kde je sebral. Ale pro x=1 je čitatel kladný a jmenovatel také. Takže jednička přece vyhhovuje.
Čitatel je kladný pro x>1/2 a jmenovatel je kladný pro x>-3. Takže dohromady je zlomek kladný pro průnik, tedy <1/2 ; oo). COž dobře dokumentuje ta samotná osa (bez tabulky).
P.S. Tu tabulku opravdu neřeším, ta je zcestná. Řeším jen tu samotnou osu, ppodle které je intzerval <1/2,oo) v pořádku.
Offline
#25 04. 02. 2011 17:50
Re: Definiční obor (info) 1.1
↑ mikl3:
Mohu toto téma uzavřít ??? je to už teď správně ???
pokud ano děkuji všem zúčastněným za podporu a hlavně , že jsme vše dotáhli k zdárnému cíli !!! ;)
calis
Všichni se v něčem předstihujeme, proto se od sebe učíme, je to lidské, nic lidského mi není cizí ... ;)
Offline


 je
je 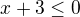 ale většina těch + nebo - je špatně
ale většina těch + nebo - je špatně
