Matematické Fórum

O.o · 16. 05. 2008 15:33 — Editoval O.o (16. 05. 2008 16:06)

Ahoj,
znovu vás otravuji, tak mne prosím neubijte.
Ještě mám snad už poslední dotaz(y).

1.
Mám zadaný příklad vypočtěte absolutní hodnotu zlomku (-2-3i)/(3-2i). Ještě mi snad nějak docvakne, že absolutní hodnota komplexního čísla je rovna $\sqrt{a_1 ^2 +a_2 ^2 }$ .
Tak bych se chtěl zeptat, jak je to u tohoto zlomku? Mám ho nejprve rozšířit, abych odstranil imaginární část ze jmenovatele a pak to nechat na dva zlomky v absolutní hodnotě a první zlomek použít jako a1 a druhý jako a2?
(Zlomek v absolutní hodnotě by pak nakonec byl např. $\frac{a}{b}+\frac{a}{b}i$ nebo to takto nejde (nevím, ejstli mi tam trochu nepřekáží ta absolutní hodnota).
Hledal jsem ostatní odkazy na kompelxní čísla tady na fóru a nějak jsem tomu úplně přesně neporozuměl. Mohl by někdo prosím pomoci?

2.
Mám zadaný příklad: x, y patří do R, vyřešte: $\frac{3-2i}{1-i}=2x+yi$
Během výpočtu mi nikde nevypadne jedna z neznámých, takže mi nakonec zůstanou součet dvou neznámých vytknutých před dvě závorky. Jestli jsem tedy neudělal numerickou chybu, jak se prosím postupuje s rovnicí, kde mi zůstanou dvě neznámé?

3.
Vypočtěte komplexní číslo "a" a určete jako absolutní hodnotu:
$a=\frac{i-1}{2}-\frac{i}{i-1}.i+1$
Stačí tady převést na společný jmenovatel a poté znovu rozšířit zlomek, aby mi vypadla imaginární část ze jmenovatele a rozdělti na dva zlomky?

4.
Jak se dá prosím určit goniometrický tvar komplexních čísel:
a) $z_1 =6i$
(tady mi nějak došli nápady, jedině snad: mám to brát jako 0+6i => a1 = 0; a2 = 6?)
b) $z_2 =\frac{1+i}{1-i}$
(znovu stačí rozšířit?)

5.
Určete 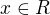$x\in R$ , tak aby pátý člen binomického rozvoje ( $\frac{2}{x}-\sqrt{x})^9$ byl roven 2016.
k=4
${9 \choose 4} \cdot (\frac{2}{x})^5 \cdot (-\sqrt{x})^4=2016\nl x^3=2$
Dále to mám rozdělat přes binomickou rovnici? Nebo jak mám zjistit x? (binomickou rovnicí mi vyjdoe x0, x1, x2 jen nevím jestli to by měl být konečný výsledek, když mám určit x, ale tady přijdu na tři x, tak nějak nevím)
// edit admina: Zapsal jsem to do TeXu, snad jsem to vydedukoval správně.

Myslím, že snad nepotřebuji, aby jste počítali celé příklady, tím bych vás nechtěl obtěžovat, jen bych potřeboval v každém příkladě nějak nakopnout (nejlépe směrem, na který se ptám).

Doufám, že vás to nebude moc obtěžovat a děkuji moc za případnou pomoc.

lukaszh

Tu dvojku by som riesil porovnavanim, kde naprv upravim zlomok:
$\frac{3-2i}{1-i}\cdot\frac{1+i}{1+i}=\frac{5-i}{2}$
dosadis do rovnice:
$\frac{5}{2}-\frac{1}{2}i=2x+yi$
Potom 2x je realna cast a yi je imaginarna cast, takisto 5/2 je realna cast a -1/2 je imaginarna cast:
$2x=\frac{5}{2}\Rightarrow x=\frac{5}{4}\nl yi=-\frac{1}{2}i\Rightarrow y= -\frac{1}{2}$
Ak je to zle opravte ma prosim.
Ta stvorka a) presne ako si povedal 0+6i, uhol bude \pi/2 a absol. hodnota 6
5 priklad riesis ako rovnicu a pouzijes vzorec pre k-ty clen:
$A_k={n\choose k-1}a^{n-k+1}b^{k-1}$

aritentd · 16. 05. 2008 15:45

1), 3) zlomky se odstrani delenim, coz je v pripade komplexnich cisel vynasobeni komplexne sdruzenym cislem ke jmenovateli
$\frac{z_1}{z_2}=\frac{z_1}{z_2}\cdot\frac{\overline{z_2}}{\overline{z_2}}$

Paulus · 16. 05. 2008 15:48

K těm zlomkům, rozšířit a vydělit (reálným číslem) např:
$\frac{i+7}{i+8}=\frac{(i+7)(i-8)}{(i+8)(i-8)}=\frac{i^2-i-56}{i^2-64}=\frac{-57-i}{-65}=\frac{57}{56}+ \frac{1}{65}i$

Paulus · 16. 05. 2008 16:04 — Editoval Paulus (16. 05. 2008 16:07)

4. a) ano b) ano

5. Nevím, kde jsi přišel na tu 4ku na začátku...
$k={9 \choose 4} \cdot (\frac{2}{x})^5 \cdot (-\sqrt{x})^4=2016\nl x^3=2\nl x=\sqr[3]{2}$

O.o · 16. 05. 2008 16:05 — Editoval O.o (16. 05. 2008 22:45)

↑ Paulus:
Promiň, to jsem jen špatně umístil tag pro začátek tex(u). Už jsem to přeurpavil, všem moc děkuji za pomoc.
Jen snad k tomu poslednímu př. Neívm jak to, žem i nedocvaklo, že z x^3 = 2 mohu udělat třetí odmocninu ze dvou (tady se nemusí řešit jestli je to +/-, jako u např: x^2 = 5 -> x = +- druhá odmocnina z pěti?).

Ještě jednou díky..

Matematické Fórum

#1 16. 05. 2008 15:33 — Editoval O.o (16. 05. 2008 16:06)

Komplexní čísla + dotaz na binomický rozvoj

#2 16. 05. 2008 15:44 — Editoval lukaszh (16. 05. 2008 15:54)

Re: Komplexní čísla + dotaz na binomický rozvoj

#3 16. 05. 2008 15:45

Re: Komplexní čísla + dotaz na binomický rozvoj

#4 16. 05. 2008 15:48

Re: Komplexní čísla + dotaz na binomický rozvoj

#5 16. 05. 2008 16:04 — Editoval Paulus (16. 05. 2008 16:07)

Re: Komplexní čísla + dotaz na binomický rozvoj

#6 16. 05. 2008 16:05 — Editoval O.o (16. 05. 2008 22:45)

Re: Komplexní čísla + dotaz na binomický rozvoj

Zápatí