Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Soustava Linerání a kvadratické rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#1 07. 02. 2011 13:24
#2 07. 02. 2011 13:25 — Editoval Tychi (07. 02. 2011 13:31)
Re: Soustava Linerání a kvadratické rovnice
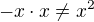 ale
ale 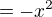
ale ty tam sekáš tolik chyb ve znaménkách, že ti nakonec i ten diskriminant vyšel správně, jen postup k němu nevede..
takže díky té chybě na začátku máš pak ve výpočtu y -7, ale mělo by být +7
a ten konec už nechápu vůbec, to jsou bludy písmenko od písmenka.
Vesmír má čas.
Offline
#3 07. 02. 2011 13:31
- Ivana Závišková


- Příspěvky: 68
- Reputace: 0
Re: Soustava Linerání a kvadratické rovnice
No právě. To je můj problém, udělám chybu ve znamínkách, ale diskriminant mě vyjde, ale postup ne :-(
Offline
#5 07. 02. 2011 13:32 — Editoval Dana1 (07. 02. 2011 13:33)
- Dana1
- Host
Re: Soustava Linerání a kvadratické rovnice
↑ Ivana Závišková:
Nevzdávaj sa, aj ten predchádzajúci príklad si môžeme prejsť - len musíš presne povedať, ktorý krok Ti nie je jasný. Ja mám čas do 15,00.
#7 07. 02. 2011 13:35
- Ivana Závišková


- Příspěvky: 68
- Reputace: 0
Re: Soustava Linerání a kvadratické rovnice
↑ Dana1:
Já se nevzdávám, jen už toho mám dost. Sedím na tím každý den do půl noci a nic z toho. Vždycky tam nadělám nějaký nesmyslný chyby. Nejhorší je, že kdyby se to člověk naučil nechtěl, tak se nedivím. Ale já se to naučit a pochopit chci a nic
Offline
#8 07. 02. 2011 13:37
- Ivana Závišková


- Příspěvky: 68
- Reputace: 0
Re: Soustava Linerání a kvadratické rovnice
↑ Tychi:
Včak tohle mám i já akorát se špatným znamínkem
Offline
#9 07. 02. 2011 13:37 — Editoval Dana1 (07. 02. 2011 13:39)
- Dana1
- Host
Re: Soustava Linerání a kvadratické rovnice
↑ Ivana Závišková:
Preto Ti vravím, nevzdávaj to. Uvidíš, keď vydržíš rátať, zrazu Ti to začne ísť. Matika je taká. Vždy si vysvetlený príklad urob aj sama. Držím Ti palce.
#10 07. 02. 2011 13:40
- Ivana Závišková


- Příspěvky: 68
- Reputace: 0
Re: Soustava Linerání a kvadratické rovnice
Nevěřím tomu,že mě tohle někdy půjde :-) já si ty příklady doma počítám sama, pak se napíšu, aby mi někdo řekl,kde je chyba...atd. jak mi to někdo opraví a vím, co jsem udělala špatně a přepočítám si to doma sama, pak se jen divím proč JÁ to udělala takhle , když je logický, že to má být tak a tak...
Offline
#11 07. 02. 2011 13:41 — Editoval Tychi (07. 02. 2011 14:02)
Re: Soustava Linerání a kvadratické rovnice
↑ Ivana Závišková:A o to jde, musíš se předně naučit používat ta znaménka správně, jinak ti sice shodou náhod sem tam něco vyjde, ale opravdu jen náhodou.
takže 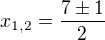
Vesmír má čas.
Offline
#12 07. 02. 2011 13:43
- Ivana Závišková


- Příspěvky: 68
- Reputace: 0
Re: Soustava Linerání a kvadratické rovnice
↑ Tychi:
No právě shodou náhod mi nějakej příklad čas od času vyjde a pak se sama divím, jak tohle je možný. Ale jak už jsem psala, když si po Vaši opravách sama přepočítám příklad, divím se proč jsem udělala tuhle a tuhle chybu, když logicky je to jinak.
Offline
#14 07. 02. 2011 13:53
- Ivana Závišková


- Příspěvky: 68
- Reputace: 0
Re: Soustava Linerání a kvadratické rovnice
Tak ten první sloupeček má být asi takto,ne?
Y=7-4
Y=3
A TEN DRUHÝ
X= 7-3
X=4
Offline
#16 07. 02. 2011 14:13 — Editoval Dana1 (07. 02. 2011 14:13)
- Dana1
- Host
Re: Soustava Linerání a kvadratické rovnice
↑ Tychi:
Lenže, Tychi, nemá tam byť x^2 = 4, keď už? ?
#17 07. 02. 2011 14:14
- Dana1
- Host
Re: Soustava Linerání a kvadratické rovnice
↑ Ivana Závišková:
Ivanka, nebolo by múdrejšie dokončiť najprv 1 príklad a potom ísť na ďalší?
#18 07. 02. 2011 14:17
Re: Soustava Linerání a kvadratické rovnice
↑ Dana1:myslím, že ne. Možná tě taky jako mě mate zápis Ivany: kvadratická rovnice je pro x a kořeny má najednou y.. správně jsou kořeny x. A y se dopočítává z té první rovnice.
taky jsem pro postupné počítání rovnic, takhle v tom Ivana musí mít v hlavě zmatek.
Vesmír má čas.
Offline
#19 07. 02. 2011 14:22
- Dana1
- Host
Re: Soustava Linerání a kvadratické rovnice
↑ Tychi:
Vieš, ja to už celé neriešim, nechcem sa medzi vás montovať - len som si všimla ten zápis, že
x^2 + 3= 7 a nasledujúci x = 7-3, x = 4.
#20 07. 02. 2011 14:24 — Editoval Cheop (07. 02. 2011 14:27)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Soustava Linerání a kvadratické rovnice
↑ Ivana Závišková: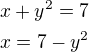
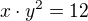
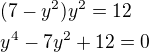
Substituce: 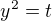
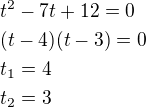
Vratka k substituci:
Pro t_1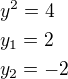
Pro t_2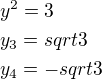
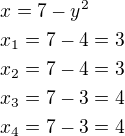
Řešení: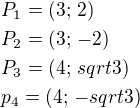
Nikdo není dokonalý
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Soustava Linerání a kvadratické rovnice (TOTO TÉMA JE VYŘEŠENÉ)


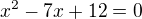
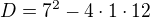
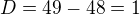
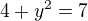 ... y=?
... y=?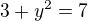 ... y=?
... y=?