Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Do elipsy o poloosách a, b vepiste obdélník nejvetsiho obsahu (TOTO TÉMA JE VYŘEŠENÉ)
#2 18. 05. 2008 16:20 — Editoval robert.marik (18. 05. 2008 16:21)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Do elipsy o poloosách a, b vepiste obdélník nejvetsiho obsahu
Offline
#3 18. 05. 2008 16:37 — Editoval Slabsí matematik (18. 05. 2008 16:39)
- Slabsí matematik
- Příspěvky: 29
- Reputace: 0
Re: Do elipsy o poloosách a, b vepiste obdélník nejvetsiho obsahu
ahoj,
z tohoto odkazu si mam vzit to, ze
misto jejich zadani 4x^2+9y^2 = 36 se ma pouzit obecne (x/a)^2 +(x/b)^2 = 1 ? a za (x/a) a (x/b) by se melo dosadit v1 a v2? diky
Offline
#5 20. 05. 2008 06:43 — Editoval robert.marik (20. 05. 2008 06:43)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Do elipsy o poloosách a, b vepiste obdélník nejvetsiho obsahu
v jejich zápise (v_1/a)^2 +(v_2/b)^2 = 1
anebo jinak (bez odmocnin)
1. Obecny bod na elipse: [x,y]
2. Plati x^2/a^2+y^2/b^2=1 tj. y^2=b^2( 1- x^2/a^2 )
3. Obsah je S=4*x*y
4. S má maximum tam, kde má maximum i S^2=16*x^2*y^2=16*x^2*b^2(1-x^2/a^2)
5. Hledám maximum funkce 
6. derivace atd ..... anebo porovnam s parabolou 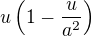 , maximum je pro
, maximum je pro 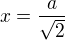
7. odpovidajici y se dopocita z 2.
8. že je to maximum je jasné z povahy úlohy, už nic dál neověřuji
Offline
#6 20. 05. 2008 06:56 — Editoval robert.marik (20. 05. 2008 08:26)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Do elipsy o poloosách a, b vepiste obdélník nejvetsiho obsahu
Druha metoda (asi lehci,a le vychazi z parametricke rovnice elipsy)
1. paramaeticke rovnice elipsy: 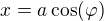 ,
, 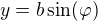 , budu brat v uvahu vrchol obdelnika v prvnim kvadrantu, tj
, budu brat v uvahu vrchol obdelnika v prvnim kvadrantu, tj 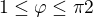
2. Obsah obdelnika 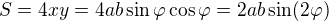
3. najdu extrém funkce 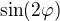 na intervalu
na intervalu 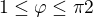 (Pomocí obrázku (modra tucna funkce) nebo pres derivaci
(Pomocí obrázku (modra tucna funkce) nebo pres derivaci 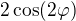 ) ten extrem je pro
) ten extrem je pro 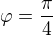
4. ze stejneho duvodu jako predtim nemusim dokazovat ze to je maximum a pisu odpoved, ze optimalni obdelnik je ten, jehoz jednim vrcholem je bod![kopírovat do textarea $ [\frac{a}{\sqrt 2}, \frac b{\sqrt 2}] $](/mathtex/9c/9c08e08d9acb0ca17001206088874871.gif) , protoze
, protoze 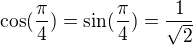
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Do elipsy o poloosách a, b vepiste obdélník nejvetsiho obsahu (TOTO TÉMA JE VYŘEŠENÉ)