Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » celociselna reseni (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 02. 2011 01:29
- kralovnicka
- Příspěvky: 122
- Reputace: 0
celociselna reseni
Ahoj,
prosim Vas, nemel byste nekdo napad, jak vyresit tento priklad?
Najdete vsechna celociselna reseni rovnice
1/x1 + 1/x2 + 1/x3 + 1/x4 = 1
pro ktera plati 3 *je mensi nebo rovno* x1 *je mensi nebo rovno* x2 *je mensi nebo rovno* x3 *je mensi nebo rovno* x4
dekuji!
Offline
- (téma jako vyřešené označil(a) FailED)
#2 14. 02. 2011 06:38 — Editoval Honzc (14. 02. 2011 06:47)
Re: celociselna reseni
↑ kralovnicka:
Jedno řešení je nasnadě:
x1=x2=x3=x4=4
Další:
x1=x2=3,x3=x4=6
Víc jich myslím nebude (ale nevím to jistě)
Offline
#4 14. 02. 2011 09:01
- kralovnicka
- Příspěvky: 122
- Reputace: 0
Re: celociselna reseni
diky moc, ale jak jste na to prisli?
Offline
#5 14. 02. 2011 10:35 — Editoval tomis33 (14. 02. 2011 10:36)
Re: celociselna reseni
Neviem či je to možné riešiť aj ináč ako úvahou.
Všetky korene musia byť väčšie prípadne rovné číslu 3... ľavá strana preto nemôže byť nikdy väčšia ako 4/3.
Preto stačí skúšať kombinácie nižších koreňov...
vieš že 1/3 + 1/6 = 1/2
taktiež 1/4 + 1/4 = 1/2
z toho vytvoríš tie 3 riešenia
Koreňom nikdy nemôže byť 5, nakoľko sčítaním 1/5 s inými 3 zlomkami asi nedostaneš len tak ľahko 1
Ďalším riešením už môžu byť len možnosti, keď zvolíš 2 najväčšie prvé 2 sčítance... Teda 1/3 + 1/3 ... k nim prirátaš ďalší relatívne väčší 1/4 (1/6 to byť už nemôže, ten výsledok už máme).... posledný sčítanec bude 1/12
preto 4. riešenie je x1=x2=3; x3=4; x4=12
Offline
#6 14. 02. 2011 12:35 — Editoval FailED (14. 02. 2011 12:37)
Re: celociselna reseni
↑ kralovnicka:
Můžeme řešit takhle: - z toho aspoň jedno číslo (tedy
- z toho aspoň jedno číslo (tedy  ) musí být nejvýš 4, kdyby byla všechna větší, součet převrácených hodnot by byl menší než 1.
) musí být nejvýš 4, kdyby byla všechna větší, součet převrácených hodnot by byl menší než 1.
Podobně postupujeme dál až k  .
.
Všechna řešení jsou opravdu  .
.
Offline
#7 14. 02. 2011 18:40
- kralovnicka
- Příspěvky: 122
- Reputace: 0
Re: celociselna reseni
↑ FailED:
takze za x1 dosadim od 1 do 4 a za x2, x3, x4 libovolna cisla? a tak to budu delat potom i s x2, x3, x4? dekuji moc!
Offline
#8 14. 02. 2011 19:40 — Editoval FailED (14. 02. 2011 19:41)
Re: celociselna reseni
↑ kralovnicka:
Od 3 do 4 :) dál postupuješ stejně, např. když je  , je
, je  a z toho musí být aspoň jedno menší nebo rovno
a z toho musí být aspoň jedno menší nebo rovno  - tedy aspoň jedno musí být nejvýš 4. Tím jsme dostali, že pro
- tedy aspoň jedno musí být nejvýš 4. Tím jsme dostali, že pro  platí jedna z možností
platí jedna z možností 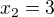 nebo
nebo  .
.
Offline
#9 15. 02. 2011 06:31
- kralovnicka
- Příspěvky: 122
- Reputace: 0
Re: celociselna reseni
↑ FailED:
jo uz mi to doslo, dik moc! :)
Offline
#10 15. 02. 2011 17:32
- check_drummer

- Příspěvky: 5181
- Reputace: 106
Re: celociselna reseni
Podobná úloha je k dispozici zde:
http://forum.matweb.cz/viewtopic.php?id=26633
"Máte úhel beta." "No to nemám."
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » celociselna reseni (TOTO TÉMA JE VYŘEŠENÉ)
