Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 02. 2011 16:38
Obracení zlomku
Nůžete někdo poradit podle čeho je možné obracet zlomek?
Uploaded with ImageShack.us
vysvětlení že je to převracené násobení mi tu poněkud nejde do hlavy...
Offline
- (téma jako vyřešené označil(a) sait-cz)
#5 26. 02. 2011 17:13 — Editoval Dana1 (26. 02. 2011 17:33)
- Dana1
- Host
Re: Obracení zlomku
↑ sait-cz:
Nerozumiem otázke. Prevrátiť zlomok znamená (ako povedal už BakyX) zameniť navzájom čitateľa a menovateľa, aj u zložených zlomkov. Možno by bolo dobré dať konkrétny príklad.
Myslíš, že keď urobíš 1/x nedostaneš to isté, ako keď zameníš čitateľ a menovateľ navzájom?
Tebe sa to úplne nepodarilo, ale možno si to dobre myslel...
#6 26. 02. 2011 19:50 — Editoval Dana1 (26. 02. 2011 21:12)
- Dana1
- Host
Re: Obracení zlomku
↑ sait-cz:
Myslím, že žiadne 1/x zapisovať netreba, proste vymeníš navzájom čitateľ s menovateľom, это всё.
#9 26. 02. 2011 20:00 — Editoval mikl3 (26. 02. 2011 20:01)
Re: Obracení zlomku
↑ sait-cz: aha, tak tohle chápu, ale nemyslím si (co jsem zatím viděl), že by se to na hodně školách řešilo takhle, toto řešení je pěkné, ale obvykle jsem to počítal, že jsem si udělal společného jmenovatele a sečet la pak jel a podmínky
jinak k příkladu: je to zajímavé ano, využívá se tam toho, že 
jinak přeci to nemusíš řešit substitucí pokud se toho bojíš, můžeš to udělat, že sloučíš zlomky (jeden převedeme a pak sečteme) a vynásobíš jmenovatelem a bude to
Offline
#10 26. 02. 2011 20:05 — Editoval mikl3 (26. 02. 2011 20:06)
Re: Obracení zlomku
↑ sait-cz: tak pokud jsi ve 4. ročníku, tak tohle by měla být samozřejmost
ano koukej:  a to si přepíšeme jako násobení a to už umíš ne?
a to si přepíšeme jako násobení a to už umíš ne?
Offline
#11 26. 02. 2011 20:05 — Editoval Dana1 (26. 02. 2011 20:06)
- Dana1
- Host
Re: Obracení zlomku
↑ sait-cz:
Máš tam stále chybu medzi tými dvoma "rovná sa", (t+1)/(2t) = 1/ [(2t) / (t+1)]
Je tam len napísané, že tie zlomky na pravej a ľavej strane sú prevrátené, čo je vidno na prvý pohľad. Symbol 1/x sa číta prevrátená hodnota
x, aby sa to nemuselo hovoriť, takto to môžeš chápať..
Keď vidíš takúto rovnicu, že tie zlomky majú ako keby prehodené čitatele s menovateľmi, 1 zlomok vždy označ x a miesto toho prevráteného zlomku
vždy napíš 1/x.
#14 26. 02. 2011 20:21
#16 26. 02. 2011 20:25 — Editoval mikl3 (26. 02. 2011 21:06)
Re: Obracení zlomku
↑ sait-cz: ten prostřední výraz nemohu dát na mínus 1, to bych porušil rovnost
ale v jiném příkladu mohu takže (asi se netrefím podle tvých myšlenek):  tohle myslíš?
tohle myslíš?
Offline

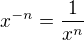
 upraveno pro tazatele
upraveno pro tazatele