Matematické Fórum

Bilbo · 19. 05. 2008 03:06

Ahoj, potřeboval bych poradit s dalšími příklady z anal. geometrie, tady je druhý:

Vzdálenost mimoběžek p: x = 7 + t, y = 3 + 2t, z = 9 - t a q: 3 - 7s, y = 1 + 2s, z = 1 + 3s je rovna?

Má vyjít 2 * 21^(1/2)

Taktéž mnohokrát děkuju.

Alesak · 19. 05. 2008 12:20

↑ Bilbo:
vis jak se to dela ve stereometrii?

Bilbo · 19. 05. 2008 13:35

Nevím, ale potřeboval bych spíše početní postup, u rovnoběžných přímek by to nebyl problém, zaráží mě ty mimoběžky.

Alesak · 19. 05. 2008 15:13

↑ Bilbo:
bez toho prave pocetni postup nevymyslis. dela se to tak, ze se najde rovina, ktera je rovnobezna k jedny primce, a zaroven obsahuje druhou primku. pak akorat najdes vzdalenost primky od roviny. tady je normalovej vektor ty roviny skalarni soucin smerovejch vektoru tech dvou primek.

liquid · 20. 05. 2008 22:17 — Editoval liquid (20. 05. 2008 22:20)

↑ Alesak:
moh bys to pls rozvest?
mame treba krychli ABCDEFGH

jak treba udelam tu rovinu z primek:

DB
a
C a stred EG

jaka rovina teda bude obsahovat jedu primku a na dalsi bude rovnobezna?

Alesak · 20. 05. 2008 22:38

no, musis znat kriterium rovnobeznosti primky a roviny. primka p je rovnobezna s rovinou kdyz ta rovina obsahuje aspon jednu primku rovnobeznou s primkou p.

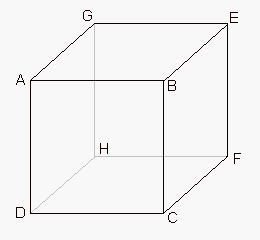
ta rovina je v tutom pripade C, stred EG a stred GH. prisel sem na to tak ze sem si primku DB posunoval aby se mi nejak pekne protla s primkou C a stred EG. posunul sem si ji teda na sted GH a X, kde X lezi na poloprimce FE, a lezi kus nad E. a pak akorat nejak urcis vzdalenost primky a roviny, coz tady neni zrovna snadny.

jaca · 20. 05. 2008 23:45

Takze z parametrické rovnice si vyjádříž přímky p, q a body P,Q. Vypočítáš si vektor přímky PQ=(-4,-2,-8). A hodíš to do vzorečku pxqxPQ/pxq (nahoře smíšený součin, dole vektorový) a vyjde to:)

Bilbo · 21. 05. 2008 01:10

Díky moc.

vok · 22. 05. 2008 13:58

A není jednodušší určit pouze vzdálenost těch dvou bodů P a Q (vlastně délka úsečky |PQ| )? Vyšel mi úplně stejný výsledek, a je to mnohem jednodušší než ty postupy, které jste tady psali. Tak se chci zeptat, jestli je to možné takto vypočítat, a nebo je to jenom náhoda, že to tak vyšlo??

Bilbo · 23. 05. 2008 02:59

Zkusil bych se ještě připojit k poslednímu příspěvku. Teď jsem to počítal a vážně správný výsledek odpovídá vzdálenosti bodů P a Q. Je to jenom náhoda nebo to tak u těchto příkladů vychází vždycky?

Matematické Fórum

#1 19. 05. 2008 03:06

Analytická geometrie přímek a rovin 2

#2 19. 05. 2008 12:20

Re: Analytická geometrie přímek a rovin 2

#3 19. 05. 2008 13:35

Re: Analytická geometrie přímek a rovin 2

#4 19. 05. 2008 15:13

Re: Analytická geometrie přímek a rovin 2

#5 20. 05. 2008 22:17 — Editoval liquid (20. 05. 2008 22:20)

Re: Analytická geometrie přímek a rovin 2

#6 20. 05. 2008 22:38

Re: Analytická geometrie přímek a rovin 2

#7 20. 05. 2008 23:45

Re: Analytická geometrie přímek a rovin 2

#8 21. 05. 2008 01:10

Re: Analytická geometrie přímek a rovin 2

#9 22. 05. 2008 13:58

Re: Analytická geometrie přímek a rovin 2

#10 23. 05. 2008 02:59

Re: Analytická geometrie přímek a rovin 2

Zápatí