Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 04. 03. 2011 16:32 — Editoval Dana1 (04. 03. 2011 16:33)
- Dana1
- Host
Re: význam Komplexních čísel
↑ sait-cz:
Myslíš praktický význam, alebo ide o niečo iné, teoretické?
Napr. tu, časť použitie.
#3 04. 03. 2011 16:43 — Editoval sait-cz (04. 03. 2011 16:58)
Re: význam Komplexních čísel
teoretický umím vypočítagt ale co prakticky kč znamená a komplexně sdružené čislo nějak nechápu ,text že je to pro to abychom mohli počítat s odm. s minuskem je jasné i u mocniné řady po 4 ,ale co komplexně sdružené čílso znamená jasné není...
Offline
#4 04. 03. 2011 19:03
Re: význam Komplexních čísel
Zdravím,
komplexně sdružené číslo k číslu z je takové číslo, jehož imaginární část má opačné znaménko než imaginární část čísla z.
Např. čísla 2+3i a 2-3i jsou komplexně sdružená.
Komplexně sdružených čísel lze využít při dělení komplexních čísel.
Všichni lidé jsou blázni, jenom já jsem letadlo.
Offline
#5 04. 03. 2011 19:09
Re: význam Komplexních čísel
já doporučuji vyznačit si do gaussovy roviny komplexní číslo a k němu číslo komplexně sdružené
význam (jestli jsem to správně pochopil) byl hlavně přisoudil počítání s těmito čísly, když ti někdo zadá 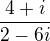 tak víš, že rozšíříš komplexně sdruženým jmenovatelem, uvedl jsem příklad se zadáním: upravte komplexní číslo do algebraického tvaru
tak víš, že rozšíříš komplexně sdruženým jmenovatelem, uvedl jsem příklad se zadáním: upravte komplexní číslo do algebraického tvaru
Offline
#6 04. 03. 2011 20:01
Re: význam Komplexních čísel
Komplexně sdružené číslo je asi něco, co se při výpočtech hodí tak často, že si to nakonec zasloužilo vlastní název a značku. Nemyslím, že se dá snadno najít nějaký příklad "ze života" jako to jde třeba u záporných čísel (dluh) nebo zlomků (krájení dortu na části). Ostatně, už u reálných čísel je zřejmě problém s praktickým příkladem -- nebo někdo dokáže vysvětlit, kde v ulici/samoobsluze najdu něco jako pi či odmocninu ze dvou?
Hlavní hezká vlastnost je ta, že 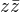 má nulovou imaginární složku a nezápornou složku reálnou -- je to takový způsob, jak se dostat zpátky do reálných čísel. Dá se pak třeba hezky definovat norma komplexního čísla jako
má nulovou imaginární složku a nezápornou složku reálnou -- je to takový způsob, jak se dostat zpátky do reálných čísel. Dá se pak třeba hezky definovat norma komplexního čísla jako  , přičemž ta odmocnina je normální reálná odmocnina, a díky tomu, že
, přičemž ta odmocnina je normální reálná odmocnina, a díky tomu, že 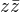 má nezápornou reálnou složku, tak po odmocnění mám opět reálné číslo. Že norma je vzdálenost z od počátku v Gaussově rovině je asi celkem vidět.
má nezápornou reálnou složku, tak po odmocnění mám opět reálné číslo. Že norma je vzdálenost z od počátku v Gaussově rovině je asi celkem vidět.
Já bych komplexní sdružení viděl jako jenom takovou pomocnou operaci -- pomocnou, ale zato velmi důležitou a častou.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
