Matematické Fórum

Wolframius

Ahoj fyzici,

potrebujem poradiť. Snáť mi aspoň s jedným príkladom pomôžete. Stačí postrčiť aby som sa mohol aj ja trápiť a nemusel to celé opísať.

1. Koleso s polomerom R sa otáča tak, že uhol otočenia $\varphi$ závisí od času podľa rovnice $\varphi = A+Bt+Ct^2+Dt^3$ , kde B=1 s^-1 a C=1 s^-2 a D=1 s^-3. Vypočítajte polomer kolesa, ak na konci druhej sekundy sa normálové zrýchlenie bodov na obvode kolesa rovnalo an=3,46*10^2 ms^-2.

Výsledok = 102m

2.Teleso padá z veže výšky h s nulovou počiatočnou rýchlosťou. Druhú polovicu dráhy prejde za čas 0,8s. Aká je výška veže?

Výsledok = 36,46m

3. Nájdite uhlové zrýchlenie telesa, ak v čase $t_1=2s$ od začiatku pohybu vektor celkového zrýchlenia bodu na obvode kolesa zvieral s vektorom rýchlosti uhol alfa=60°!

Výsledok = 0,43 rads^-2

Ďakujem
wolf

jelena · 06. 03. 2011 11:11

Zdravím,

fyzikům pozdrav vyřídím (přiležitostně).

Jelikož máš pouze 1. příspěvek, ještě jednou pravidla.

K problému - nerovnomětný pohyb po kružnici, volný pad si, prosím, vyhledej. Potom po jedné úloze do tématu + vlastní návrh. Děkuji.

Téma označím za vyřešené.

Wolframius

Ďakujem za rady a ospravedlňujem sa za neprečítanie pravidiel aj keď som potvrdil, že som si ich prečítal.

Ak teda ešte môžem: Ďakujem za vzorce, ale tie mi z riešením až tak veľmi nepomôžu ak neviem aké mám použiť aby som došiel ku konečnému riešeniu.

1. príklad som rátal takto:

$a_n=\frac{d\varphi}{dt}*r$
po dosadení:
$3,46*10^2=\frac{1+2+4}{2}*r$ (urobil som prvú deriváciu $\varphi=A+Bt+Ct^2+Dt^3 \Rightarrow d\varphi=B+Ct+Dt^2$ a dosadil za BCD)
$346=\frac{7}{2}*r$
$346=3,5*r \Rightarrow r=98,86m$

Ak som počítal správne, tak výsledok mal byť takýto, ale nezhoduje sa s výsledkom, ktorý uviedli za správny pre našu kontrolu.

2. príklad som rátal takto:

$v=-\frac{1}{2}gt^2$
$v=\sqrt{2gh}$
Potom:
$v=v$
$-\frac{1}{2}gt^2=\sqrt{2gh}$
$(-\frac{1}{2}gt^2)^2=2gh$
$h=\frac{(-\frac{1}{2}gt^2)^2}{2g}$
teda:
$h=\frac{(-\frac{1}{2}*9,81*0,8^2)^2}{2*9,81}$
$h=0,502272m$

Zrejme som mal vypočítať ešte niečo aby mi výsledok vyšiel 36,46m a nie 0,5m

3. príklad som riešil takto:

Pri tomto príklade som nevedel začať. Nerozumiem tomu uhlu.

Môžeš mi prosím pomôcť?

Ďakujem a ešte raz sa chcem ospravedlniť za nedodržanie podmienok registrácie na tento web.
wolf

zdenek1 · 06. 03. 2011 13:08

↑ Wolframius:
1) $a_n=\frac{d\varphi}{dt}r$ špatně
$a_n=\left(\frac{d\varphi}{dt}\right)^2r$ správně

$\frac{\text{d}\varphi}{\text{d}t}=B+2Ct+3Dt^2$

zdenek1 · 06. 03. 2011 13:14

↑ Wolframius:
2. Všechno zcela mimo.
$\frac h2=\sqrt{gh}t+\frac12gt^2$

zdenek1 · 06. 03. 2011 13:26

↑ Wolframius:

$\frac{a_n}{a_t}=\tan\alpha$
$\frac{\frac{v^2}r}{\frac vt}=\tan\alpha$
$\frac vrt=\tan\alpha$ Protože $\frac vr=\omega$ a $\varepsilon=\frac\omega t$
dostaneš
$\omega=\frac{\tan\alpha}t\ \Rightarrow\ \varepsilon=\frac{\tan\alpha}{t^2}$

Wolframius · 06. 03. 2011 14:02

zdenek1 napsal(a):
↑ Wolframius:
1) $a_n=\frac{d\varphi}{dt}r$ špatně
$a_n=\left(\frac{d\varphi}{dt}\right)^2r$ správně

$\frac{\text{d}\varphi}{\text{d}t}=B+2Ct+3Dt^2$

Po dosadení dostanem toto:

$a_n=\left(\frac{d\varphi}{dt}\right)^2*r$
$346=\left(1+2t+3t^2\right)^2*r$
$346=\left(17\right)^2*r$
$346=289r$
$r=1,197231834m$ alebo som sa zasa sekol ako pri derivácii?

zdenek1 · 06. 03. 2011 14:07

↑ Wolframius:
Nesekl. Spíš se někdo spletl při psaní a místo 1,2 napsal 102

Wolframius · 06. 03. 2011 14:24

zdenek1 napsal(a):
↑ Wolframius:
2. Všechno zcela mimo.
$\frac h2=\sqrt{gh}t+\frac12gt^2$

Ďakujem teda za čas s prvým a tretím príkladom :).

Môžeš mi prosím napísať ako si dospel k tomu druhému vzorcu?
Vyšla mi kvadratická rovnica a následne záporná výška, čo je hlúposť.

zdenek1 · 06. 03. 2011 14:35

↑ Wolframius:
Těleso padající z výšky $h$ , bude mít ve výšce $\frac h2$ rychlost $v_0=\sqrt{2g\frac h2}=\sqrt{gh}$
Nyní si představ druhou část pohybu jako zrychlený pohyb s počáteční rychlostí 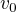$v_0$
$s=v_0t+\frac12gt^2$ , kde $s$ je ta zbývající půlka výšky
$\frac h2=\sqrt{gh}\cdot t+\frac12gt^2$
kvadratickou rovnici samozřejmě dostaneš

Řešení Odkaz nakonci dole

Wolframius

Ďakujem veľmi pekne :). Vážim si, že mi niekto úplne cudzí na druhej strane pomohol s výpočtom domácej úlohy :). Som rád, že som sa nad tým musel zamýšľať a neokopíroval som to celé. Ďakujem za tvoj čas ;).

wolf

Matematické Fórum

#1 06. 03. 2011 10:26 — Editoval Wolframius (06. 03. 2011 11:46)

Fyzika I. - Kinematika

#2 06. 03. 2011 11:11

Re: Fyzika I. - Kinematika

#3 06. 03. 2011 12:32 — Editoval Wolframius (06. 03. 2011 12:36)

Re: Fyzika I. - Kinematika

#4 06. 03. 2011 13:08

Re: Fyzika I. - Kinematika

#5 06. 03. 2011 13:14

Re: Fyzika I. - Kinematika

#6 06. 03. 2011 13:26

Re: Fyzika I. - Kinematika

#7 06. 03. 2011 14:02

Re: Fyzika I. - Kinematika

zdenek1 napsal(a):

#8 06. 03. 2011 14:07

Re: Fyzika I. - Kinematika

#9 06. 03. 2011 14:24

Re: Fyzika I. - Kinematika

zdenek1 napsal(a):

#10 06. 03. 2011 14:35

Re: Fyzika I. - Kinematika

#11 06. 03. 2011 15:14 — Editoval Wolframius (06. 03. 2011 15:15)

Re: Fyzika I. - Kinematika

Zápatí