Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 06. 03. 2011 18:08 — Editoval koudis (06. 03. 2011 18:10)
#3 06. 03. 2011 18:29 — Editoval koudis (06. 03. 2011 18:46)
Re: integrovanie
↑ renewal:
to zadani plochy je trosku divne :) ...
vysla mi trosku jinak (mozna taky proto, ze tam mas spatne meze .. misto -2 tam je 2 ...)![$\left[ -\frac{x^3}{3} + \frac{x^2}{2} + 6x \right]^3_{-2} = (-\frac{27}{3} + 0.5\cdot 3 + 18) - ( \frac{8}{3} - 1 -12) = \frac{21}{2} + \frac{31}{3} = \frac{125}{6}$](/mathtex/fd/fd3d14e4651826b77e81fc69878ab003.gif "kopírovat do textarea")
... (mozna tam mam taky nekde bug...)
Offline
#5 06. 03. 2011 23:23
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: integrovanie
↑ renewal:
Zdravím,
je třeba do jednoho tématu umísťovat jen jednu úlohu, potom je problém najit, kterou (-1) máš na mysli.
jak doporučuje kolega ↑ koudis:: dělení jmenovatele člen po členu ( na závěr jsi ztratil 1):
------------------------------------------
(3) rozpracováno máš dobře, je třeba upravit vícepatrovou odmocninu na mocninu tak, aby se dál použit vzorec pro integral od (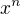
),
tedy
Také bych poprosila o větší snahu o čítelnost zápisu a použití místních možností pro zápis.
Další kontroly již prosím do jiného tématu. Děkuji.
Offline