Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 03. 2011 12:43
Pravděpodobnost
Zdravím, řeším právě nějaký příklady na pravděpodobnost, ale moc si nevím rady.
př1:
Ve velkém množství písemek se vyskytují dva typy chyb, A a B. Pravdepodobnost, že
v písemce bude chyba A je 0,1 a pravdepodobnost, že tam bude chyba B je 0,2. Pravdepodobnost,
že v písemce budou obe chyby zároven je 0,05. Urcete pravdepodobnost,
že v písemce bude pouze chyba A, nikoliv chyba B.
To vůbec netuším, zkoušel jsem všechno možné a nic.... Vyjít by to mělo 5%
př2:
Pocátecní stadium rakoviny se vyskytuje u každých trí z jednoho tisíce Americanu.
Pro vcasné zjištení byl vyvinut velmi spolehlivý test. Pouze 5% zdravých pacientu má
výsledky pozitivní (falešný poplach) a pouze 2% nemocných mají výsledek negativní.
Pokud by se tento test použil pro vyšetrení celé americké spolecnosti a všichni ti, kterí
by meli pozitivní výsledky by byli hospitalizováni za úcelem klinického vyšetrení, kolik
% z nich bude skutecne mít rakovinu?
No určil jsem, že:
je nemocen (opravdu) H1 P(H1)=3/1000 P(A|H1)=0.02
není nemocen H2 P(H2)=997/1000 P(A|H2)=0.05
je označen A
pak jsem větou o úplné pravděpodobnosti došel k 0,04991, nevím co dál, či zda jsem vůbec postupoval správně... Vyjít by mělo 5,6%
př3:
Zamýšlíte koupit v autobazaru vuz jisté znacky. Je ovšem známo, že 30% takových vozu
má vadnou prevodovku. Abyste získali více informací, najmete si mechanika, který je
po projíždce schopen odhadnout stav vozu a jen s pravdepodobností 0,1 se zmýlí. Jaká
je pravdepodobnost, že vuz, který chcete koupit, má vadnou prevodovku
a) predtím, než si najmete mechanika?
b) jestliže mechanik odhadl, že vuz je dobrý?
a) to je podle mě 30% ze zadání
b) netuším, chtěl jsem to nějak doloval také přes větu o pravděpodobnosti a pak Baysovou větou, ale nemůžu to nějak zapsat
označil jsem
špatný vůz H1 P(H1)=30% P(A|H1)=0.1
dobrý vůz H2 P(H2)=70% P(A|H2)=0.1
chybně označen A
nevím jak dál, vůbec mi to nevychází....
Díky alespoň za náznak řešení.
Offline
#2 01. 03. 2011 14:23
Re: Pravděpodobnost
↑ NetFenix:
Ten prvy priklad je mozno jednoduchsi ako sa zda.
Zamyslime sa nad tym, co to presne znamena, ze v pisomke je iba chyba A a nie chyba B. Je to vlastne to iste, ako ked povieme ze je tam chyba A a zaroven tam nie su obidve chyby zaroven. Takze od pravdepodobnosti 0,1 odpocitame 0,05 a dostavame 0,05.
Offline
#3 01. 03. 2011 14:34 — Editoval mikee (01. 03. 2011 14:34)
Re: Pravděpodobnost
↑ NetFenix:
Co sa tyka druheho prikladu, tak je dost mozne ze nerozumiem zadaniu, pretoze ten vysledok 5,6% sa mi zda velmi nerealny. Je to preto, lebo ten test sa zda byt na zaklade toho opisu pomerne spolahlivy (inak povedane: pravdepodobnost ze sa pomyli, je velmi mala). Na druhej strane vysledok hovori, ze zo vsetkych ludi, ktori maju rakovinu na zaklade testu, ju ma naozaj iba 5,6%, cize podla toho by sa test pomylil v takmer 95% pripadoch.
No a k tvojmu postupu, ak P(A|H1) znamena ak tomu dobre rozumiem pocet ludi s rakovinou, ktori maju pozitivny vysledok, tak by to nemalo byt 0,02 ale 0,98.
Offline
#4 01. 03. 2011 14:58
Re: Pravděpodobnost
Offline
#5 07. 03. 2011 16:54
- Beda70
- Host
Re: Pravděpodobnost
↑ mikee:
Už dávno jsem si odvykl spoléhat se v pravděpodobnosti (v psti) na "selský rozum". Zaokrouhlený výsledek 5,6% je správně. Když si spočítáš P(A) zmíněnou větou o úplné psti, zjistíš že podíl těch kdo rakovinu skutečně mají je mnohem menší než podíl těch kdo ji nemají:
P(A 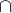 H1) = 0,00294 ; P(A
H1) = 0,00294 ; P(A 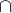 H2) = 0,04985
H2) = 0,04985
To jen na okraj, pro snazší vstřebání výsledku ktrý se ti nezdá možný.
Pro NetFenixe:
Nesmíš vařit z holé vody. Když se naučíš pár základních vzorců, půjde to samo. V př. 2 musíš použít Bayesovu větu:
P(H1/A) = P(A/H1)×P(H1) / ( P(A/H1)×P(H1) + P(A/H2)×P(H2) )
(ve jmenovateli je věta o úplné psti). Vychází 0,05569.... .
#6 07. 03. 2011 17:33
- Beda70
- Host
Re: Pravděpodobnost
↑ NetFenix:
Př. 3b)
Jo, na to jde taky nasadit Bayese. Tvůj problém spočívá v tom že nešikovně (příliš složitě) volíš náhodný jev A jako "mechanik se zmýlí". Už v tomto označení je skryta závislost na tom jaký ten vůz doopravdy je. Jako náhodný jev musíš volit něco tak říkajíc elementárního, např.:
A1 - mechanik označí vůz jako špatný
A2 - mechanik označí vůz jako dobrý
(A1 a A2 jsou opačné jevy, stejně jako H1 a H2.) Pak je P(A2/H1) = 0,1 a P(A2/H2) = 0,9. Byesem z toho vychází P(H1/A2) = 0,03 / (0,03 + 0,63) .
Zamysli se nad tím. Přeložit smysluplně slovní formulaci úlohy do matematické symboliky je typický a hlavní kámen úrazu!
