Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 09. 05. 2008 13:46
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: průběh funkce
def obor:
je tam ln, odmocnina a jmenovatel, musi byt x>0
vzhledem k takovemu nesymetrickemu definicnimu oboru ani neuvazujeme o sudosti nebo lichosti - neni ani jedno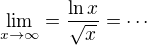
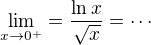
tyhle dvě limity (jedno a l'Hospitalovo pravidlo, jedna na pravidlo o podilu limit) vam reknou, jak to vypada s asymptotama
Staci takto?
Offline
#3 14. 05. 2008 10:13
Re: průběh funkce
pomohl by mi nekdo to vyřešit dál? jakto vypada dál, abych dospěl ke grafu, jak urcim spojitost funkce, prvni derivaci, stacionarni body, intervaly monotonie a lokalni extrémy, druha derivace, intervaly ryzi konkav/konvek, asymptoty, poradi mi alespon neco někdo?? pls:)
Offline
#4 14. 05. 2008 10:41
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: průběh funkce
Funkce je elementarni, tj je spojita na celem definicnim oboru, tj na intervalu (0,nekonecno)
Derivaci umite vypocitat? je potreba pouzity vzorec pro derivaci podilu a pak to je snadne. Zkuste napsat, jak Vam vychazi derivace.
Offline
#6 14. 05. 2008 11:26 — Editoval robert.marik (14. 05. 2008 11:26)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: průběh funkce
Je to dobre, to prece vite z toho old.mendelu.cz
ted je ptreba najit stacionarni body, tj resit rovnici 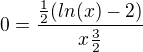 ktera je ekvivalentni rovnici
ktera je ekvivalentni rovnici 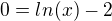
Offline
#8 14. 05. 2008 11:49
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: průběh funkce
resim rovnici 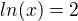
postup je popsany treba tady: http://matematika.havrlant.net/forum/vi … hp?id=1781 prispevek 2
na logaritmus se utoci exponencialni funkci
Offline
#11 14. 05. 2008 12:00 — Editoval robert.marik (14. 05. 2008 12:44)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: průběh funkce
ln(x)=2
exp(ln(x))=exp(2)
x=exp(x) pisu exp(2) pro e^2, aby to slo lip videt
O.K.
mame na realne ose body x=0 (kraj definicniho oboru) a x=e^2, mame tedy v definicnim oboru dva podintervaly (0,e^2) a (e^2, nekonecno)
z kazdeho podintervalu vezmu cislo a dosadim do derivace. jaka vyjdou znamenka?
editace - oprava preklepu
Offline
#14 14. 05. 2008 12:48
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: průběh funkce
derivace je ale neco jineho, sam jste ji spocital ..... 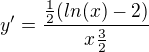
v intervalu (0,e^2) lezi treba x=1. kolik je derivace v jednicce? je kladna? jestli ano, funkce na tomto intervalu roste. Jestli ne, klesa
v intervalu (e^2,nekonecno) lezi treba x=e^3. kolik je derivace v e^3? je kladna? jestli ano, funkce na tomto intervalu roste. Jestli ne, klesa
doporuduji prohlednout nejake resene priklady. http://old.mendelu.cz/~marik/prez/prubeh-cz.pdf
Offline
#15 14. 05. 2008 12:51
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: průběh funkce
ted pujdu na schuzi a nebudu tu, ale potom se vratim. ale treba to uz ani nebude potreba ....
Offline
#16 18. 05. 2008 14:20
- Slabsí matematik
- Příspěvky: 29
- Reputace: 0
Re: průběh funkce
Ahoj , nema nahodou ta prvni derivace byt jeste s minusem pred zlomkem?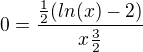 .
.
Pokud by se pote dosadila jednicka do prvniho intervalu ( 0 , e^2) vyslo by, ze funkce v tomto intervalu roste.
Muzes prosim uvest na kterou limitu jsi pouzil l ´hospitalovo pravidlo a na kterou pravidlo podilu a jaky je presny postup?
Jaky je podle tebe inflexni bod? je to bod e na 8/3?
Vim, ze funkce neni ani licha ani suda, ale jak to dokazu pomoci matematickych overeni. Slovni komentar mi asi stacit nebude.
dekuji a preji pekny den
Offline
#17 18. 05. 2008 14:40 — Editoval robert.marik (18. 05. 2008 14:40)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: průběh funkce
1. chybi tam opravdu minus, ja jsem to poprve nepocital, jenom jsem pouzil vysledek, ktery napsal puvodni tazatel
2. inflexe je v x=e^(8/3)
3. Sudost lichost se vyvrati protiprikladem (Kontrabeispiel): f(1)=0, f(-1) neexistuje - protoze nejsou ani stejne ani se nelisi znamenkem, funkce neni ani suda ani licha
4. v nule zprava je limita minus nekonecno lomeno nulou a to "lomeno nulou" jde k nule ze strany kladnych cisel, limita je proto minus nekonecno.
v nekonecnu to je nekonecno lomeno nekonecnem a pocita se klasicky lHospitalovym pravidlem.
Offline
#18 25. 05. 2008 13:34 — Editoval tomajs (25. 05. 2008 13:35)
Re: průběh funkce
Tak jsem se do toho zase pustil a zatim jsem dosel tady, potrebuju aby mi to nekdo zkontroloval a poradil jak to bude s tema limitama u bodu 4. a jak urcim ty stacionarni body a monotonii a extremy atd. prosim o kontrolu:
http://tomajs.chytrak.cz/IMAGE_272.jpg
dekuji
Offline
#21 25. 05. 2008 14:56
Re: průběh funkce
ja si myslim ze je to jedno ne, je to ekvivalentni, mam to dobre, je to i polde toho http://old.mendelu.cz/ zkontrolovane....spis nevim co dál to urceni intervalu ryzi monotonie a lokalnich extremu
Offline
#23 25. 05. 2008 15:01
Re: průběh funkce
dobre a vis jak se urci ty stacionarni body, je to s te 1. derivace, se vezme ten cicatel a polozi se nule a vyresi se jako rovnice a vyjde mi jedno x a druhe vezmu z definicniho oboru?? nebo jak se to resi i ty extremy a monotonie, kdy je rostouci atd.
Offline
#24 25. 05. 2008 15:04
Re: průběh funkce
stacionarni body dostanes tak, ze polozis prvni derivaci rovno nule. o extremech se rozhodne z druhe derivace. intervaly, kdy je funkce rostouci a klesajici zjistis take z prvni derivace - tam, kde je zaporna, funkce klesa, naopak kde je kladna, funkce roste. ok?
Offline
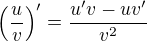 , popletl jsi poradi derivaci v citateli
, popletl jsi poradi derivaci v citateli