Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#29 25. 05. 2008 18:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: průběh funkce
↑ tomajs:
znamenko derivace pred bodem e^2 je kladne, za bodem se meni na zaporne, v bode x= e^2 nastava lokalni maximum funkce, funkce je rostouci na intervalu (0, e^2), funkce je klesajici na (e^2, + oo) - to jsou rovnez intervaly monotonnosti.
Je to tak srozumitelne?
Offline
#32 25. 05. 2008 19:02 — Editoval tomajs (25. 05. 2008 19:04)
Re: průběh funkce
takze druha derivace mi vysla: ![$-\frac{\frac{1}{4}{}{}(3ln(x)-8]}{x^{\frac{5}{2}} }$](/mathtex/ad/ad2f4bef7784350323681cd82d671404.gif "kopírovat do textarea")
jak mam ted urcit konkávnost a konvexnost?
vypocitam z druhe derivace kriticke body, tj. resim rovnici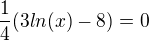 
polozim ji nule a vyjde mi kriticky bod: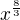 
je to tak???? jaka teda bude ta funkce konkavni, konvexni na jakych intervalech, diky za odpoved popripade opravu
Offline
#33 25. 05. 2008 19:42
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: průběh funkce
↑ tomajs:
Bod podezrely z inflexe by mel dopadnout takto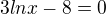 
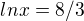
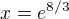- toto je bod podezrely z inflexe - overujeme znamenko 2. derivace pred - (dosaduji treba e^1) 2. derivace je zaporna, po prechodu pres tento bod 2. derivace je kladna, bod x = e^ (8/3) je inflexni, funkce je konkavni na intervalu (0, e^(8/3) ) a konvexni na intervalu (e^(8/3) , + oo)
Offline
#35 25. 05. 2008 19:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: průběh funkce
↑ tomajs:
Ostatni jsou daleko lepsi, ale jsi je zrejme odrovnal tvrzenim v prispevku 27 (ale to je detail) :-)
http://www.gymvod.cz/s/Image/matematika/Asymptoty.pdf - tady je postup, jak na asymptoty - vytvor zapisy pro asymptoty, budes hledat limity f(x) /x. Tipuji to na l´Hospitala. Tak zatim drzim palce :-)
Offline
#36 25. 05. 2008 20:36 — Editoval tomajs (25. 05. 2008 20:41)
Re: průběh funkce
takze prvni pocitam svisle asymptoty: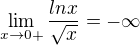
vyresil by mi to nekdo:)
pak tedy ty šikmé: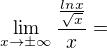
tohle bych taky potreboval vyresit no a tohle limita se bude rovnat treba A, a pak se udela jeste jedna limita:
je to tak ne? chapu to dobre polde toho pdf, potreboval bych to vyresit prosim.....:)
Offline
#37 25. 05. 2008 21:06 — Editoval jelena (25. 05. 2008 21:06)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: průběh funkce
↑ tomajs:
vertikalni asymptota je x=0, limita zleva k O- neni nutna, neni tam Df.
pro sikmou (asymptota se smernici) - pouze pro x se blizi + oo, pouzijes l´Hospitala, A - jak jsi oznacil vychazi 0,
uplne posledni vzorec nema "deleno x" a ma byt take pouze k + oo. take l´Hospitalem vychazi 0, asymptota se smernici ke tedy y= 0* x + 0 = 0.
OK?
Offline
#38 26. 05. 2008 15:39
Re: průběh funkce
jelena napsal(a):
↑ tomajs:
vertikalni asymptota je x=0, limita zleva k O- neni nutna, neni tam Df.
pro sikmou (asymptota se smernici) - pouze pro x se blizi + oo, pouzijes l´Hospitala, A - jak jsi oznacil vychazi 0,
uplne posledni vzorec nema "deleno x" a ma byt take pouze k + oo. take l´Hospitalem vychazi 0, asymptota se smernici ke tedy y= 0* x + 0 = 0.
OK?
muzes mi prosim napsat jak si dospela k te sikme symptote? nejak nevim jak na to, pocital jsem to, ale kdyz pouziju l´Hospitala zderivuju tak stejne nejak nedojdu k te 0
a toho posledniho vzorce si taky nevim rady.....pls napis mi postup
Offline