Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 20. 05. 2008 11:53 — Editoval robert.marik (20. 05. 2008 11:56)
- robert.marik
- Einstein
- Příspěvky: 999
- Reputace: 1
Re: Cauchyovy úloha
Obecne reseni mate? Hleda se pres charakteristickou rovnici (obecne reseni asociovane homogenni rovnice) a potom bud metodou variace konstant, nebo odhadem partikularniho reseni (jedno z partikularnich reseni je linearni funkce)
PS: anebo to potrebuejte v matlabu? http://matematika.havrlant.net/forum/vi … hp?id=2745
Offline
#4 20. 05. 2008 12:33
Re: Cauchyovy úloha
pak hledam partikularni reseni - pouziji metodu neurcitych koeficientu, protoze prava strana rovnice je linearni polynom. hledam tedy partikularni reseni ve tvaru 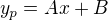 , spocitam prvni, druhou a treti derivaci
, spocitam prvni, druhou a treti derivaci 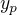 a dosadim do puvodni rovnice a vypocitam koeficienty A, B. nakonec dopocitam reseni vyhovujici pocatecnim podminkam.
a dosadim do puvodni rovnice a vypocitam koeficienty A, B. nakonec dopocitam reseni vyhovujici pocatecnim podminkam.
Offline
#5 21. 05. 2008 13:21
Re: Cauchyovy úloha
↑ robert.marik:
v tom matlabu tje snad takhle
close all; clear all;
echo off; clc;
syms a b c d x y;
y=zeros(1,100);
f= dsolve('D3y-6*D2y+12*Dy-8*y=x-2','y(0)=0','Dy(0)=2','D2y(0)=1', 'x')
for i=1:301
t=(i-1)/100;
y(i) = subs(f,t);
end;
cas=0:0.01:3;
subplot(3,1,1)
plot(cas,y);
options = odeset('RelTol',1e-4);
[T,Y] = ode45(@fce,[0 3],[0 2 1],options);
options = odeset('RelTol',1e-7);
[T2,Y2] = ode45(@fce,[0 3],[0 2 1],options);
subplot(3,1,2)
plot(T,Y(:,1),'.',T,Y(:,1),'-',T2,Y2(:,1),'.',T2,Y2(:,1),'--');
%hold
subplot(3,1,3)
plot(T,Y(:,1),'.',T,Y(:,1),'-',T2,Y2(:,1),'.',T2,Y2(:,1),'--')
==========================
druhy mfile
fce.m
function dy=fce(t,y)
dy = zeros(3,1);
dy(1) = y(2);
dy(2) = y(3);
dy(3) = t-2+6*y(3)-12*y(2)+8*y(1);
ale vubec si nejsem jist
Offline
#7 25. 05. 2008 23:23
Re: Cauchyovy úloha
y´´´-6y´´+12y´-8y = x-2
yOH = C1e^2x+C2*x*e^2x+(C3*x^2)*e^2x
yp = a+ b*x + c*x^2 + d*x^3
yp´ = b + 2*c*x +3*d*x^2
yp´´ = 2*c + 6*d*x
yp´´´ = 6*d
6*d - 12*c - 36*d*x + 12*b + 24*c*x + 36*d*x^2 - 8*a - 8*b*x - 8*c*x^2 - 8*d*x^3 = x-2
6*d - 12*c + 12*b - 8*a = -2
-36*d*x + 24*c*x - 8*b*x= 1*x
36*d*x^2 - 8*c*x = 0
- 8*d*x^3 = 0
d=0
c=0
b=-1/8
a=1/16
yp = 1/16 -1/8*x
co mam delat s tema pocatecnima podminkama ?
Offline
#10 26. 05. 2008 14:39
Re: Cauchyovy úloha
hmm tak za trest ze sem to odevzdal pozde sem dostal dalsi priklad :( ....
y´´´+y´=-x*sinx y(0)=1, y(0)´=0, y(0)´´=2
chtel sem se jen zeptat kdyz koreny jsou 0 a +-i pak homogeni strana je
Yoh=C1+C2*sinx+C3*cosx ?
a partikularni reseni Yp=(Ax+B)*sinx+(CX+D)*cosx ??
dekuji za odpoved
Offline

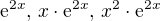

 C1=0 ............
C1=0 ............