Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 03. 2011 15:57 — Editoval joinusman (20. 03. 2011 15:57)
Válec
Dobrý den,
nevím si rady s touto úlohou:
Do válce je vyhloubena dutina v podobě rotačního kužele, mají
společnou podstavu a vrchol kužele leží v polovině druhé podstavy.
Plášť kužele je roven plášti válce.
Jaký je objem nově vyhloubeného tělesa?
Vypočítal jsem si z rovnosti plášťů, že platí:
v = s/2 , ale nevím, jak postupovat dále. Děkuji za radu.
Offline
- (téma jako vyřešené označil(a) joinusman)
#2 20. 03. 2011 16:16
- Dana1
- Host
Re: Válec
↑ joinusman:
Vo vyhĺbenom kuželi je výška rovná polovici výšky valca a dá sa napísať Pytagorova veta pre trojuholník s preponou s (strana kužeľa) a odvesnami
v/2 (polovica výšky valca) a r (polomer podstavy kužeľa. Miesto v dosadíš Tebou získaný vzťah medzi v a s. Vyjadríš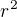 
pomocou s a dosadíš
do vzťahu pre objem kužeľa.
#3 20. 03. 2011 17:05
Re: Válec
↑ Dana1:
Dobrý den,
chci se omluvit za nejasnost v zadání: Otázka je, jaký je objem nového tělesa, které vznikne po vyhloubení (to
asi znamená objem válce minus objem kužele).
Dvě věci tak úplně nechápu. Proč je výška kužele rovna polovině výšky válce, neměly by být stejné?
A jakým způsobem prosím potom využiji vyjádřené r pomocí s, když veličiny s ve vzorci pro objem
nevyužívám? Děkuji
Offline
#4 20. 03. 2011 17:31 — Editoval Dana1 (20. 03. 2011 18:32)
- Dana1
- Host
Re: Válec
↑ joinusman:
Nepozorne som pozrela zadanie, ospravedlňujem sa. Ešte raz sa na celé pozriem.
Objem kužeľa je vždy 1/3 objemu valca s rovnakou podstavou aj výškou. Výsledné teleso má teda objem rovný 2/3 objemu valca.
Výsledný vzťah sa dá zapísať iba všeobecne. Napísal si, že v= s/2. Z Pytagorovej vety vyplýva, že 
, tak keď dosadíš do vzťahu
pre objem obidva vzťahy (v aj r^2), dostaneš výsledný objem vyjadrený pomocou jedného parametra s.