Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 03. 2011 18:24
Úhel protnutí křivek
Zdravím,prosím o vyřešení příkladu, který je zadán takto :Pod jakým úhlem se protínají křivky?
1)y = x^2 a x = y^2
2) y=-2/2x a y = x^2 −1
Moc prosím o celý výpočet a zápis u obou podpříkladů, protože jaksi netuším,co přesně s tím :) Děkuju moc předem :)
Offline
#7 26. 03. 2011 18:42 — Editoval mikl3 (26. 03. 2011 18:44)
Re: Úhel protnutí křivek
Hansss napsal(a):
Zdravím,prosím o vyřešení příkladu, který je zadán takto :Pod jakým úhlem se protínají křivky?
a
a
to soustavy jsou, proč a jak bys je ještě dělal? to nechápu, prostě máš 2 soustavy tak řeš
řešení té 1.
Offline
#11 26. 03. 2011 19:52
- Dana1
- Host
Re: Úhel protnutí křivek
↑ Hansss:
Keď dosadíš za x do prvej rovnice, dostaneš na ľavej strane y a na pravej 
Prenesieš neznámu na 1 stranu, vyjmeš, rozložíš podľa "vzorca"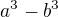 
a dostaneš súradnice dvoch priesečníkov...
#12 26. 03. 2011 19:56
Re: Úhel protnutí křivek
↑ Hansss: vypočítat tyhle soustavy není vůbec těžké, ale já se zcela otevřeně zeptám: jsi líná, nebo to neumíš?
znám lidi, kteří by dělali to samé z důvodu lenosti a i lidi, kteří dostali za úkol něco, co nechápou, celé studium opisují, prolézají, zbaběle plácají...
tak co? já se ptám, protože to je asi jako tohle: chci vypočítat volný pád, ale neumím upravit rovnici, vytknout, odmocnit, odečíst...
Offline
#13 26. 03. 2011 20:00
Re: Úhel protnutí křivek
↑ Dana1:ja jsem to napsala jako y^4-y=0,potom jsem vytkla y a napsala to takto: y(y^3-1)=0 a to znamená,že z toho y před závorkou mám y=0.A závorku rozložím podle vzorce na (y-1)(y^2+y+1)=0 a z té první závorky mi vyjde y=1,ale ta druhá mi nejde rozložit:(
Offline
#14 26. 03. 2011 20:05
Re: Úhel protnutí křivek
↑ mikl3: já nejsem lína,matematika mě ve škole baví,ale vždycky když narazím na nějaký problém tak se zaseknu,znervozním a nejsem schopná to přejít a počítat dál:( prostě detailista:( a vím,že kolikrát jsou to drobnosti nebo jen se zbytečně přepíši v čísle a je to :(
Offline
#15 26. 03. 2011 20:08
Re: Úhel protnutí křivek
↑ Hansss: dobře, takyže potřebuješ určit souřadnice, ve kterých mají obě funkce stejnou hodnotu, tedy kde se protínají
jestli jsi někdy řešila soustavu rovnic lineárních graficky, tak to jsou průsečíky přímek, když se to řeší početně, tak se vyřeší soustava, tak ji vyřeš
(existuje spousta metod) a (bavím se o jedné soustavě), vyjdou ti dvě xové a 2 ypsilonové a to jsou ty průsečíky, u druhé soustavy obdobně
Offline
#16 26. 03. 2011 20:10 — Editoval claudia (26. 03. 2011 20:11)
Re: Úhel protnutí křivek
Hansss napsal(a):
↑ Dana1:ja jsem to napsala jako y^4-y=0,potom jsem vytkla y a napsala to takto: y(y^3-1)=0 a to znamená,že z toho y před závorkou mám y=0.A závorku rozložím podle vzorce na (y-1)(y^2+y+1)=0 a z té první závorky mi vyjde y=1,ale ta druhá mi nejde rozložit:(
Ono to také má pouze dvě reálná řešení, to je v pořádku. Teď si k nim ještě "dopočítej" to x :-) V bodech x pak budeš určovat ony derivace.
Offline
#17 26. 03. 2011 20:11
Re: Úhel protnutí křivek
↑ mikl3:omlouvám se,už mi to docvaklo a když jsem dopočítala i xove souřadnice tak mám T1(0,0) a T2(1,1) a když jsem potom udělala rovnice tečen pro y=x^2 tak jedna mi vyšla t:y=0,tzn. že i úhel je 0 stupňů a ta druhá mi vyšla t:y=2x-1,tzn. 63,43 stupňů,je to tak? :)
Offline
#20 26. 03. 2011 20:25
Re: Úhel protnutí křivek
↑ Hansss: no já jsem chtěl vědět něco malinko jiného - ptám se: křivky si "zjednodušíme" na přímky či polopřímky, ono to tak skutečně asi bude, protože v průsečících mají stejné souřadnice a pak jednoduše určíme úhel?
Offline