Matematické Fórum

jardas · 27. 03. 2011 16:01

↑↑ claudia:

tady je vidět, že jsem na matematiku moc hloupej... a že z ní mam čtyřky.. ten poslední krok je fakt ošklivý... to jsem si ani neuvědomil, že absolutní hodnota nesmí být záporná....

claudia · 27. 03. 2011 16:03

To neznamená, že ty ostatní jsou správně :-) Tak šup, opravit, dokud jsem online :-)

jardas · 27. 03. 2011 16:10

↑ claudia:

myslim, že to bude na dlouho ... prosim tě , buď tu co nejdýl.... můj skype je ,, jardas.typ a moje icq je 557851057 " pokusim se to zkusit vypočítat, co nejrychlejš, abych tě nezdržoval..

jardas · 27. 03. 2011 16:19

↑ claudia:

když se tak koukam zpětně do sešitu... nikde nemam zobáček , aby ukazoval na levou stranu...

claudia · 27. 03. 2011 16:22

Proboha. Zobáček...

Jestli tě to dráždí, můžeš řešit nerovnici

$0 > -1 \cdot x^{-2} + 1 &$

jardas · 27. 03. 2011 18:13

↑ claudia:

Prosím, napiš mi to.. nepřišel jsem na to.. , ale už jsem se dostal ke 4. bodu na tom prvnim příkladu :) a Váš kolega mi napsal, že je to dobře... :)

claudia · 27. 03. 2011 18:34

Když nechceš počítat se mnou, mohu si to spočítat sama, máš pravdu :-)

$f'(x) = -1 \cdot x^{-2} + 1 &< 0\\ 1&<\frac{1}{x^2}\\ x^2&<1\\ \left|x\right|&<1\\ x &\in $-1,0$ \cup $0,1$$

tzn. klesající je v intervalu $\[-1,0\)$ a $\(0, 1\]$

zjevně v levém okolí bodu -1 je rost., v pravém je kles., tedy v -1 má lok. max, analogicky v 1 lok. min.

inflex. body analogicky řešení nerovnic pro druhou derivaci $f''=\frac1{x^3}$

kde se mění znaménko je inflexní bod; kovexní je funkce na intervalu, pokud má druhá derivace ve vnitřních bodech intervalu kladnou hodnotu, analogicky konkrávní pokud zápornou
(zde inflexní body nejsou, konvexní je v kladné části osy, konkávní v záporné)

průsečíky s osami funkce nemá

asymptotu má v plus i mínus nekonečnu 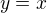$y=x$ , protože:

$\lim_{x\to \pm\infty}\frac{x+\frac{1}{x}}{x}=\lim_{x\to \pm\infty} \frac{1+\frac{1}{x^2}}{1}=1$
$\lim_{x\to \pm\infty}x+\frac{1}{x} - x=\lim_{x\to \pm\infty} \frac{1}{x} = 0$

limity jsou

$\lim_{x\to\infty} f(x) = \infty,\;\lim_{x\to-\infty} f(x) = -\infty,\;\lim_{x\to 0_+} f(x) = \infty,\;\lim_{x\to 0-} f(x) = -\infty$

a graf bys z toho měl zvládnout

z mé strany k tomuto příkladu vše