Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 03. 2011 15:37
- stuart clark

- Příspěvky: 1015
- Reputace: 7
cubic equation
If 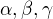 be the roots of the equation
be the roots of the equation 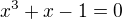 .Then Calculate value of
.Then Calculate value of 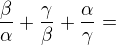
Offline
- (téma jako vyřešené označil(a) byk7)
#2 28. 03. 2011 12:23 — Editoval musixx (28. 03. 2011 12:56)
Re: cubic equation
In general, those tasks are used to lead to so called symmetric polynomials, and Viete's formulas (consult e.g. Wikipedia for details).
But it is not this case, since there is no symmetric polynomial in the numerator of a fraction  , while there is a symmetric polynomial in its denominator.
, while there is a symmetric polynomial in its denominator.
Moreover, your number is not well-defined, since it depends on an order of the roots.
Example 1, an illustrative one: , and
, and 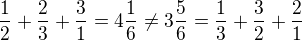 .
.
Example 2: it could be shown that your number is either 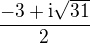 or
or 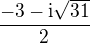 .
.
Offline
#3 28. 03. 2011 13:52 — Editoval Pavel (28. 03. 2011 13:56)
Re: cubic equation
↑ stuart clark:
Remark: Similar problem can be found at http://forum.matweb.cz/viewtopic.php?id=21735
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline