Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#651 03. 03. 2011 15:23 — Editoval Dana1 (05. 03. 2011 17:52)
- Dana1
- Host
Re: LaTeXové pískoviště
#653 05. 03. 2011 08:13 — Editoval Dana1 (05. 03. 2011 08:51)
- Dana1
- Host
Re: LaTeXové pískoviště
↑ johny0222:
1. Najprv si podľa návodu zostav niekoľko integrálov sám, aby si pocítil, o čom to je.
2. Jednotlivé už napísané časti môžeš odosielať a kontrolovať priebežne, či sa nestala nejaká chyba. Kilometrový zápis sa zle kontroluje.
3. EDIT: Zápis Ti skontrolovala Jelena.
#654 05. 03. 2011 08:42
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: LaTeXové pískoviště
↑ johny0222:
Zdravím a děkuji za ochotu :-)
K tomu, co píše ↑ Dana1: (děkuji) - kontroluji, prosím, že počet levých závorek a počet pravých závorek je stejný - tedy každá { ma svou}, také \( má \). Ještě jsem smazala * pro násobení.
Je to v pořádku? 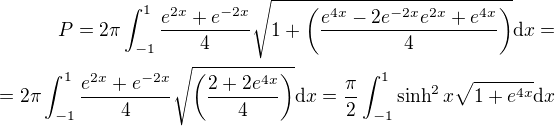
Zda je to matematicky správně, jsem nekontrolovala.
↑ Dana1: kolega Hanzy určitě odpoví - užívá si prázdnin (obježdí okolní kopce s umělým sněhem, sjezdy mu jdou hodně dobře) a trochu cvičí matematiku, klavír a bicí :-)
----------
Omlouvám se, mně nepřisluší odpovídat v tomto tématu.
Offline
#655 05. 03. 2011 08:47 — Editoval Dana1 (05. 03. 2011 08:55)
- Dana1
- Host
Re: LaTeXové pískoviště
↑ jelena:
Ďakujem, ja som to opraviť nedokázala, zdalo sa mi tam všeličo poprehadzované... viem o tom ešte príliš málo. Ahoj, kolegu Hanzyho zdravím a závidím mu...
#656 06. 03. 2011 09:56 — Editoval Dana1 (07. 03. 2011 13:35)
- Dana1
- Host
Re: LaTeXové pískoviště
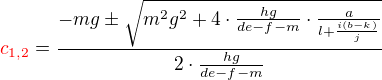
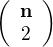
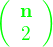




#657 07. 03. 2011 21:57
#658 08. 03. 2011 10:07
- Dana1
- Host
Re: LaTeXové pískoviště

#659 08. 03. 2011 11:27
#660 08. 03. 2011 11:29
#662 08. 03. 2011 12:24 — Editoval Dana1 (08. 03. 2011 12:38)
- Dana1
- Host
Re: LaTeXové pískoviště

#663 08. 03. 2011 17:49
#664 08. 03. 2011 17:50
#665 08. 03. 2011 17:54
Re: LaTeXové pískoviště
↑ zdenek1:
Teraz ti celkom nerozumiem..Keď dám Alt Gr + W, čo mi robí |, tak mi to jednoducho ukáže, ale potom mi to hneď zmaže, keď kliknem inde.
1^6 - 2^6 + 3^6 = 666
Offline
#666 08. 03. 2011 18:02
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: LaTeXové pískoviště
↑ zdenek1:
Myslím, že body by se měly sázet bezpatkovým neskloněným písmem. Ale nemůžu k tomu najít zdroj, kde jsem to viděl. Je to tak?
Offline
#667 08. 03. 2011 18:08 — Editoval zdenek1 (08. 03. 2011 18:12)
Re: LaTeXové pískoviště
↑ Pavel Brožek:
Nevím, já pravidla sazby zas až tak podrobně neznám. Reagoval jsem na centimetry psané v matematickém módu. (příspěvek 10:07)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#668 08. 03. 2011 18:10
#669 08. 03. 2011 20:19
Re: LaTeXové pískoviště
↑ zdenek1:
namiesto ALT+124, stačí jednoducho ťuknúť AltGr+W resp. ALT+CTRL+W
To len tak pomimo ;-)
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#670 11. 03. 2011 17:59
#672 11. 03. 2011 18:18
Re: LaTeXové pískoviště
↑ Dana1: dakujem , fakt uz si spominam .... davno som nerobil s latexom ....
"If you think you understand quantum mechanics, you don't understand quantum mechanics" - Richard Feynman
"Linux is like a tepee no windows, no Gates, apache inside"
Offline
#673 13. 03. 2011 09:49 — Editoval Dana1 (13. 03. 2011 09:55)
- Dana1
- Host
Re: LaTeXové pískoviště
#675 30. 03. 2011 10:56
Re: LaTeXové pískoviště
<math>C = \sum_{t=1}^{n} D\times\frac{(1+g)^t}{(1+k)^t} = D\times \left[ \frac{(1+g)}{(1+k)} +...+ \frac{(1+g)^n}{(1+k)^n} \right] </math>
<math>A\times\frac{(1+k)}{(1+g)} = D\times \left[ \frac{(1+g)^0}{(1+k)^0}+ \frac{(1+g)}{(1+k)} +...+ \frac{(1+g)^{n-1}}{(1+k)^{n-1}} + \left(\frac{(1+g)^n}{(1+k)^n} - \frac{(1+g)^n}{(1+k)^n}\right) \right]</math>
<math>A\times(1+k) = D\times(1+g)\times\left(1-\frac{(1+g)^n}{(1+k)^n}\right) + (1+g) A</math> <math>Ak = D\times(1+g)\times\left(1-\frac{(1+g)^n}{(1+k)^n}\right) + (1+g)A - A</math> <math>A(k-g) = D\times(1+g)\times\left(1-\frac{(1+g)^n}{(1+k)^n}\right)</math> <math>A = D\times\frac{(1+g)}{(k-g)}\times\left(1-\frac{(1+g)^n}{(1+k)^n}\right)</math> as, <math> n \rightarrow \infty </math> and <math> g < k </math> <math>A = D\times\frac{(1+g)}{(k-g)}</math>
Offline


![kopírovat do textarea $P(A) = P(A_1\cup A_2 \cup A_3) = 1 - [1-P(A_1)][1-P(A_2)][1-P(A_3)] = 1 - 0,8 \cdot 0,7 \cdot 0,9 = 0,496
P(D) = P(\overline A_1\cup A_2 \cup A_3) =
$](/mathtex/52/5266785dae655f61e593c4c0c35f6c03.gif)