Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Určitý integrál, nevím jak postupovat (TOTO TÉMA JE VYŘEŠENÉ)
#2 04. 04. 2011 19:35 — Editoval claudia (04. 04. 2011 19:54)
Re: Určitý integrál, nevím jak postupovat
Obecně to lze řešit Eulerovou substitucí, ale tento příklad přímo vybízí provést drobnou úpravu a použít substituci:
Pro 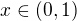 platí
platí
Dále je to jasné?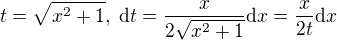

Offline
#3 04. 04. 2011 20:01
Re: Určitý integrál, nevím jak postupovat
↑ claudia:
Moc děkuju :-) a dál to mám zintegrovat rozkladem na parciální zlomky? Nebo jak se s tím vypořádat?
Offline
#5 04. 04. 2011 20:48
Re: Určitý integrál, nevím jak postupovat
↑ claudia:
Díky že mi tak pomáháš, ale jsem tak hloupá, že mi to pořád nevychází :( zintegrovala jsem to jako 2*( ln (t+1) - ln (t+1)^2 ), dosadila jsem přepočítanou mez (tedy 1 a sqrt(2) ), vyšlo mi to nějak okolo -3, ale má to vyjít 0,1024... Kde dělám chybu?
Offline
#7 04. 04. 2011 21:13
Re: Určitý integrál, nevím jak postupovat
↑ da.backer:
nechápu jak jsi na to přišel, můžeš vysvětlit? :-)
Offline
#8 04. 04. 2011 21:25 — Editoval claudia (04. 04. 2011 21:27)
Re: Určitý integrál, nevím jak postupovat
↑ katka88:
Není mi jasné, jak jsi k tomu výsledku přišla. Kdyby sis zkusila napsat postup, pravděpodobně bys našla i chybu :-)
↑ katka88:
Můžeš provést substituci 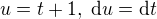 , pak
, pak
Offline
#9 04. 04. 2011 21:27 — Editoval da.backer (04. 04. 2011 21:37)
Re: Určitý integrál, nevím jak postupovat
↑ katka88:
TAk to první mám jako ty a to druhé je integrované
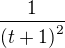 čili
čili 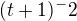 a dle vzorce
a dle vzorce 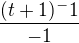 dej si za to t+1 substituci a pujde to ;)
dej si za to t+1 substituci a pujde to ;)
EDIT: Tak jak píše claudia :) omlouvám se za vstup, netušil jsem že tu jěště někdo radí takhle večer :)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Určitý integrál, nevím jak postupovat (TOTO TÉMA JE VYŘEŠENÉ)



