Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 28. 05. 2008 01:43 — Editoval xificurC (28. 05. 2008 02:09)
Re: Nekonečná řada
Dokazat to neviem, no zda sa, ze to bude spravne: Tvoje (1!+2!+...+n!)/n! je zhora ohranicene, teda stacilo by dokazat, ze sa da zhora ohranicit konkretnym cislom (napr. 2) a potom cez porovnavacie kriterium a Lebniza mas vysledok...
Edit: Hehe, este som sa hrajkal a mat. indukciou mi vyslo, ze (1!+2!+...+n!)/n! je mensie-rovne ako 2 a potom cela habadura je mensia-rovna ako  , co je uz len Leibniz...
, co je uz len Leibniz...
Offline
#6 28. 05. 2008 19:16
Re: Nekonečná řada
↑ xificurC:
Abel rika, ze kdyz  konverguje a je monotonni a
konverguje a je monotonni a 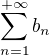 konverguje, tak rada
konverguje, tak rada 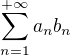 konverguje
konverguje
Offline
#7 29. 05. 2008 14:20
Re: Nekonečná řada
↑ xificurC:
Dokonce lze dokazat o neco silnejsi tvrzeni, nez to tvoje, ale zadarmo to neni, tedy ve smyslu, ze se pouzije mene trivialni prostredek nez matematicka indukce, nicmene aplikace je pravdepodobne mnohem snazsi. Plati totiz (podle Stolzovy vety, jejiz predpoklady jsou splneny u nasledujici limity)
odkud se da take pomerne rychle rici to, co tvrdis, tedy, ze studovany vyraz je mensi-roven 2. Dale pak srovnavaci a Leibnizovo kriterium davaji konvergenci puvodni rady.
Offline
#8 29. 05. 2008 14:47
Re: Nekonečná řada
↑ Tomsus:
Tak sry, my sme v skole brali, ze staci, aby bola monotonna a ohranicena, konvergencia je zase silnejsia poziadavka, teda neviem, ako to ma byt :) Kazdopadne este raz sry ;) Ako to teda bude napr. s takou radou sin n / n^2 ? Viem, ze staci porovnavacie kriterium a hotovo, ale splna takato rada abelove podmienky alebo nie?
↑ Marian:
Diky za doplnenie :)
Offline
#9 29. 05. 2008 17:29
#10 29. 05. 2008 17:35 — Editoval Tomsus (29. 05. 2008 17:49)
Re: Nekonečná řada
Jo, a rada sin n / n^2 je absolutne konvergentni - nesplnuje Abelovy podminky - protoze sin n neni konvergentni, ale protoze |sin n|<=1 pro vsechna n, da se to srovnat s 1/n^2 a ta konverguje. O malinko je zajimavejsi (sin n) / n, ta konverguje neabsolutne - protoze rada sin n ma omezenou posloupnost castecnych souctu a 1/n --> 0, tak podle Dirichleta - jo, na to jsem chtel narazit - ze Abelovo kriterium je vlastne takova modifikace Dirichletova kriteria
Offline
#11 29. 05. 2008 19:18 — Editoval Marian (29. 05. 2008 19:20)
Re: Nekonečná řada
Pro zainteresovane si dovolim jeste jednu drobnou poznamku o sume rady 
Plati totiz identita
↑ Tomsus:
Co to znamena "Ach sooooooo ....". Mam to chapat nemecky? Tedy "Ach taaaaaaak ...."?
Offline
#12 29. 05. 2008 20:25
Re: Nekonečná řada
↑ Marian:
Ano, je to "ach taaaaak". Jenom mi to konecne doslo :-)
je to zvlastni, jak casto se objevuji cisla jako pi, e, zlaty rez - treba ten soucet sin n/n (o tom jsem nevedel), soucet rady 1/n^2 je zas pi^2/6, nebo tak nejak. Takove zvlastni, az dokonce iracionalni cislo a takovy potencial :-)
Offline

 konverguje a za mam ukazat ze konverguje
konverguje a za mam ukazat ze konverguje 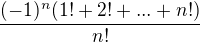
 konverguje k nule a je monotonni
konverguje k nule a je monotonni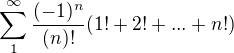 také konverguje
také konverguje