Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 05. 2008 23:08 — Editoval lopson (29. 05. 2008 23:09)
tangens a perioda?
Ahoj,
tak jsem tu o5 s goniometrií.
√3(tgx)^2 + tgx = 0 , měl bych zjistit počet všech reálných kořenů pro (-pi/2 ; pi/2). U sinusu nebo cosinusu mi to celkem jde. U tangensu to nějak vázne, hlavně moc nevím, co s periodou.
Upravil jsem: tgx(√3tgx + 1) = 0
pak tedy: tgx=0 nebo tgx=-√3/3
Nooo a teď celkem nevím jak dál. Záporný tg by měl být ve 2. a 4. kvadrantu - tak třeba perioda kPi?
Nevim no, ale pokud byste si mysleli, že je to lepší upravit na sinus s cosinem sem s tím. Ale asik by tam musely být podmínky a tak aaaaa to není moc fajn. Potřeboval bych, aby celá úprava byla co možná nejrychlejší a nejjednodušší.
Díky moc :-)
Offline
#5 29. 05. 2008 23:24
Re: tangens a perioda?
No a to mě právě celé mate, protože pro x=kpi mi vychází 1 kořen a u toho x=5/6pi + kpi mi nevychází žádný kořen. A ve výsledku mají být 2 kořeny. Pokud tedy pro (k) začínám nulou pak se tam nevejde ten druhý kořen... nebo u každého takového příkladu musím brát v potaz všechna celá čísla tedy i záporná??? A zkoušet to třeba i pro -1, -2... ???
Offline

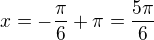 . takze klidne muzes psat
. takze klidne muzes psat 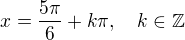
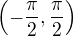 ?
? dostaneme volbou
dostaneme volbou 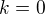 koren
koren 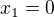
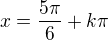 dostaneme volbou
dostaneme volbou 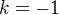 koren
koren 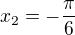 .
.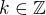 , predpokladam, ze vis, co jsou to cela cisla
, predpokladam, ze vis, co jsou to cela cisla