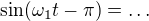Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 04. 2011 18:27 — Editoval Crusad (11. 04. 2011 18:27)
Integrál
Zdravím, mám tu problém s integrálem. 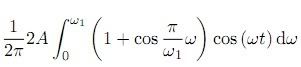 .
.
Roznásobím a první mi vyjde  , ale co s tím druhým, to netuším. Poradil by někdo?
, ale co s tím druhým, to netuším. Poradil by někdo?
Výsledek má být takový, ten můj častečný výsledek tam už je, teď je zjistit jak dojit k tomu zbytku.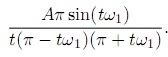
Díky za pomoc
Offline
- (téma jako vyřešené označil(a) Crusad)
#2 11. 04. 2011 21:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál
Zdravím,
2. integral - přes vzorec pro součin goniometrických funkcí 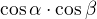 - cca v polovině seznamu vzorců.
- cca v polovině seznamu vzorců.
Stačí tak? Děkuji.
Offline