Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 04. 2011 19:33 — Editoval Ryco (13. 04. 2011 20:00)
Průběh funkce x/lnx

vyšlo mi:
 fce je lichá
fce je lichá
první derivace fce,která mi vyšla podle maw,takže je dobře.
a tady sem se zasekl u urceni stacionárního bodu,položil sem fci rovnou nule a po úpravě mi vyšlo 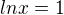 a nvm co s tím dále(
a nvm co s tím dále(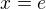 mohlo by to být tak?). Tímpádem sem nemohl zjistit jestli je fce rostoucí či klesající, tak sem se pokusil vyšetřit druho derivaci a ta mi taky nevyšla. Dál sem nepokračoval. tady přikládám moje dva pokusy o tu druhou derivaci
mohlo by to být tak?). Tímpádem sem nemohl zjistit jestli je fce rostoucí či klesající, tak sem se pokusil vyšetřit druho derivaci a ta mi taky nevyšla. Dál sem nepokračoval. tady přikládám moje dva pokusy o tu druhou derivaci
Odkaz
Prosím o pomoc =)
Offline
#3 13. 04. 2011 20:00 — Editoval Phate (13. 04. 2011 20:01)
Re: Průběh funkce x/lnx
To jsi brzo zanevrel na logaritmy :)
Jinak funkce neni licha, protoze je definovana pouze v 
Doporucuji derivace kontrolovat pomoci http://www.wolframalpha.com/
EDIT: a jsem zase pomalej :(
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#12 14. 04. 2011 14:32 — Editoval Ryco (18. 04. 2011 13:25)
Re: Průběh funkce x/lnx
tak tady posílám co jsem vyřešil prosím o kontrolu

 funkce neni ani suda ani licha
funkce neni ani suda ani licha

v intervalu: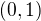 klesa,
klesa,  klesa,
klesa, 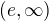 roste,
roste, 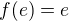 lokální minimum
lokální minimum
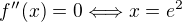 bod podezřelý z inflexe
bod podezřelý z inflexe
v intervalu: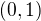 konkávní,
konkávní,  konvexní,
konvexní,  konkávní,
konkávní,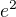 inflexní bod
inflexní bod
počítal sem i asymptoty,ty mi ale vyšli že nemá, což se mi podle grafu který u této fce vyjde moc nezdá
Offline
#14 15. 04. 2011 08:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Průběh funkce x/lnx
↑ Honzc:
Zdravím,
je to drzost, když je požadováno "vyjádření studovaných matematiků", ale tak: v 
 nebude asymptota bez směrnice (svislá), to je důsledkem, že limita funkce k 0+ je nulová. V bodě x=0 na grafu nakreslíme prázdné kolečko, ze kterého graf začne, ale def. obor tady není.
nebude asymptota bez směrnice (svislá), to je důsledkem, že limita funkce k 0+ je nulová. V bodě x=0 na grafu nakreslíme prázdné kolečko, ze kterého graf začne, ale def. obor tady není.
Může být? Děkuji.
Aby kolečko bylo zaplněno, to by se muselo dodefinovat, což se nepožaduje.
↑ Ryco:
Souhlasím s kolehou Honzc(em), že asymptota bez směrnice je v x=1, je třeba došetřit pomoci limit chování funkce zleva a zprava od této hodnoty. Asymptota se směrnici mi také nevyšla, sice k=0, ale při výpočtu q již vychází limita v nekonečnu.
Zbytek jsem nekontrolovala.
Offline

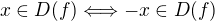
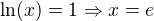


 jako
jako 
![kopírovat do textarea $\frac{lne-1}{ln^2e}=\frac{1-1}{1^2}=0 ... [e,0]$](/mathtex/70/70a97cbce521bc03ca6986943d7a9aa5.gif)
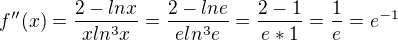


 => v bodě
=> v bodě  je lokální minimu
je lokální minimu jak sem psal výše)
jak sem psal výše)