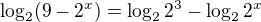Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 20. 04. 2011 17:41 — Editoval hradecek (20. 04. 2011 17:44)
Re: Logaritmická rovnice
↑ vajcoj:
Použi definíciu logaritmu...
teda: 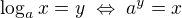
Budeš riešiť exponenciálnu rovnicu z ktorej ti vzíde kvadratická rovnica...prídeš ku dvom koreňom, ale nie každý koreň kvadratickej rovnice musí, byť výsledkom rovnice logaritmickej...
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#6 20. 04. 2011 19:13 — Editoval Dana1 (20. 04. 2011 19:24)
- Dana1
- Host
Re: Logaritmická rovnice
↑ vajcoj:
Na pravej strane má byť podľa definície to, čo je napísané za 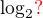
#7 20. 04. 2011 19:16 — Editoval hradecek (20. 04. 2011 19:46)
Re: Logaritmická rovnice
↑ vajcoj:
skoro :)
Ideme podľa vzorca: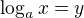
Vypíšeme si z 

Takže rovnica bude...stačí dosadiť
EDIT1: Ak by si išiel tak ako píše ↑ jrn: dostaneš tú istú exponenciálnu rovnicu...takže si môžeš vybrať. čo sa ti viac pozdáva ;-)
EDIT2: ↑ Dana1: Ďakujem, za poopravenie...malá chybička krásy...na veci to, ale nič nemení...
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline

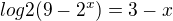 Poradíte prosím?
Poradíte prosím?