Matematické Fórum

Marian · 30. 03. 2011 10:29

Nedávno se v tématu vyskytla zajímavá trigonometrická identita. Původně jsem zamýšlel vést důkaz více elementární technikou, tj. bez využití Eulerova vztahu a následného přepisu funkce sinus prostřednictvím exponenciální funkce s komplexním argumentem.

Své řešení jsem zakládal na identitě

$\sin (nx)=2^{n-1}\cdot\prod_{k=0}^{n-1}\sin\left (\frac{k\pi}{n}+x\right ),\qquad n\in\mathbb{N}.$

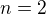Pro $n=2$ dostaneme známý vzorec pro duplikaci argumentu funkce sinus (po triviální úpravě). Podobně jsem dokazoval i případ $n=3$ a $n=4$ . Bez použití Eulerova vztahu se mi ale obecný důkaz nedaří nalézt.

Pro důkaz identity zadané v příspěvku zde stačí oddělit faktor v součinu identity výše přísušející indexu 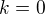$k=0$ , vydělit ním (za předpokladu jeho nenulovosti) a provést limitní přechod (třeba pro 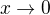$x\to 0$ ). Pak již není problém úlohu v tématu elegantně vyřešit.

Pokud máte nápady na důkaz pomocí reálné analýzy, docela by mě zajímaly.

Kondr · 04. 04. 2011 02:00

Jen idea: na levé straně je zřejmě lichá funkce, na pravé straně to získáme z rovnosti $\sin\left (\frac{k\pi}{n}+x\right )=\sin\left (\frac{(n-k)\pi}{n}+x\right )$ . Navíc lze jistě obě strany psát ve tvaru P(sin(x),cos(x)), kde P je homogenní polynom stupně n. U mnoha členů musí mít díky lichosti nulový koeficient -- pro liché n lze obě strany psát ve tvaru
$cos(x)Q(sin(x))$ , pro sudé n ve tvaru $Q(sin(x))$ . Dva polynomy stupně $n$ rovnají, pokud jsou stejné jejich funkční hodnoty v $n+1$ bodech. Pokud za $x$ zvládneme dosadit $n+1$ hodnot majících různý sinus a pro každou z nich ověřit rovnost, máme vyhráno (pro lichá $n$ stačí dokonce $n$ hodnot, neboť stupeň polynomu je nižší, ale hodnotu $\pi/2$ nemůžeme použít). Pro hodnoty tvaru $\frac{k\pi}n$ rovnost platí zřejmě, stačí nám tak ukázat, že platí pro jediné další $x$ , tedy např. že funkce mají stejnou amplitudu. To už se mi nepovedlo :(

andrew · 22. 04. 2011 16:12

↑ Marian:

Výše uvedenou identitu lze snadno odvodit následujícím způsobem (nebudu vše rozepisovat dopodrobna, nechť si laskavý čtenář rozepíše sám). Bohužel, lehce se dotkneme komplexních čísel při hledání kořenů "kvadratické" rovnice
$z^{2n}-2z^n\cos(na)+1=0$ kde $n\in \mathbb{N}, a\in \mathbb{R}$ .

Pakliže si uvědomíme, že každý polynom lze rozložit na součin kořenových činitelů, můžeme psát
$z^{2n}-2z^n\cos(na)+1 = \prod_{k=0}^{n-1}\left(z^2-2z\cos(a+\frac{2k\pi}{n}) +1 \right)$

Po dosazení $z=1, a = 2x$ a menších úpravách dostaneme

$\sin (nx)=2^{n-1}\cdot\prod_{k=0}^{n-1}\sin\left( \frac{k\pi}{n}+x\right)$

Matematické Fórum

#1 30. 03. 2011 10:29

Trigonometrická identita

#2 04. 04. 2011 02:00

Re: Trigonometrická identita

#3 22. 04. 2011 16:12

Re: Trigonometrická identita

Zápatí