Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 04. 2011 15:55
- Aquabellla
- Moderátorka Bellla
- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Vzorec pro součet n-členů AP
Zdravím, jak by se odvodil a dokázal vzorec pro součet n-členů aritmetické posloupnosti?
Sn = n/2 . (a1 + an)
Důkazy u posloupností se nejčastěji dělají matematickou indukcí, ale i přesto, že vzorec znám, jsem se nedohrabala konce... předem díky :-)
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
- (téma jako vyřešené označil(a) Aquabellla)
#2 24. 04. 2011 16:03 — Editoval vajcoj (24. 04. 2011 16:04)
Re: Vzorec pro součet n-členů AP
seřadíš si členy řady vzestupně a pod to napíšeš řadu ještě jednou, ale sestupně:
a1 a2 a3 ........ an
an a(n-1) a(n-3) .........a1
Součet členů nad sebou je vždy stejný => (an + a1), máme tu 
takových dvojic. Protože jsem ale rozepsal tu posloupnost dvakrát, tak vzorec pro součet jedné řady bude Sn = n/2 * (a1 + an)
Offline
#3 24. 04. 2011 16:08
- Aquabellla
- Moderátorka Bellla
- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Vzorec pro součet n-členů AP
↑ vajcoj:
aha, díky moc, už jsem to pochopila :-) a jak by se to zpětně dokázalo, že to opravdu platí?
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#4 24. 04. 2011 16:15 — Editoval Dana1 (24. 04. 2011 16:21)
- Dana1
- Host
Re: Vzorec pro součet n-členů AP
↑ Aquabellla:
Čo presne máš na mysli? Myslím, že uvedený postup od kolegu je priamy dôkaz. ešte by sa možno mohlo explicitne ukázať, že jednotlivé súčty sú naozaj rovnaké...
#5 24. 04. 2011 16:19
- Aquabellla
- Moderátorka Bellla
- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Vzorec pro součet n-členů AP
↑ Dana1:
Máme striktního profesora, který chce, abychom uměli všechno dokazovat... a i odvození vzorců se musí zpětně dokázat jako jistotu, že jsme ho odvodili správně. Většinou se u posloupností dokazuje indukcí, ale nejde se mi dostat ke správnému závěru u druhého kroku
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#6 24. 04. 2011 16:35 — Editoval Dana1 (24. 04. 2011 18:33)
- Dana1
- Host
Re: Vzorec pro součet n-členů AP
↑ Aquabellla:
Nie som odborník na dôkazy...
Predpokladáš, že pre n je rovnosť splnená.
Ideš ju dokázať pre n+1. Myslím, že ak ukážeš, že súčet pre n + 1 sa dá zapísať ako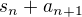 
, tak si dôkaz spravila. Áno?
Lebo toto ukázať viem...
A pozri, čo som našla (len hovorí o rade, neviem, prečo...):
Je to odtiaľto: Odkaz
#7 24. 04. 2011 16:51
- Aquabellla
- Moderátorka Bellla
- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Vzorec pro součet n-členů AP
↑ Dana1:
Děkuju mockrát, ani se nedivím, že jsem na takový důkaz nepřišla sama :-)
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline