Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 23. 04. 2011 12:22 — Editoval Rumburak (23. 04. 2011 12:27)
Re: goniometricky tvar komplexneho cisla
↑ rimer:
Jak už jsem napsal, především máš špatně přechod od  k
k  ,
,
správný mezivýsledek měl být  .
.
Nyní najdeme společné řešení goniometrických rovnic  ,
,  na intervalu
na intervalu  .
.
Zdůrazňuji, že musejí být splněny OBĚ tyto rovnice (hledané číslo  je pak na uvedeném intervalu jednoznačně určeno).
je pak na uvedeném intervalu jednoznačně určeno).
EDIT. Takže je-li v zadání  , potom úprava na
, potom úprava na  je správně a ty gon. rovnice budou
je správně a ty gon. rovnice budou ,
,  na intervalu
na intervalu  , což je řešitelné ve IV. kvadrantu.
, což je řešitelné ve IV. kvadrantu.
Offline
#9 23. 04. 2011 20:33
- Dana1
- Host
Re: goniometricky tvar komplexneho cisla
↑ rimer:
Ak nenastala niekde chyba, mne to vyšlo:
Ak  tak v I. kvadrante
tak v I. kvadrante 


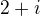 .
.

 tusim ze by mal byt v 4. kvadrante
tusim ze by mal byt v 4. kvadrante ,
,  .
. v I. kvadrantu, pak
v I. kvadrantu, pak  je ve IV. kvadrantu, takže
je ve IV. kvadrantu, takže  a tedy
a tedy  .
.