Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 04. 2011 17:55
pravděpodobnost při hodu 3 mincí
Zdravím. Potřebovala bych trošku pomoci s úlohou. Hodíme 3x mincí. Určete pravděpodobnost, že padne-li poprvé líc, padne potřetí stejná mince jako podruhé.
Původně jsem příklad řešila jako náhodný jev, ale pak mě napadlo, jestli to spíš není podmíněná pravděpodobnost. Můžete mi někdo, prosím, poradit?
Díky
Offline
- (téma jako vyřešené označil(a) dexka)
#2 27. 04. 2011 18:15
Re: pravděpodobnost při hodu 3 mincí
Nejak nechapu zadani, "že padne-li poprvé líc, padne potřetí stejná mince jako podruhé. " Sak preci hazu 3x jednou minci, cili mince padne vzdy stejna, protoze jinou nemam, takze pravdepodobnost 1 :)
Predpokladam ale ze chytak to neni, nebo ano?
Pokud to chytak neni a ptame se ktere strana padne, zalezi na tom, zda se jedna o jev zavisly ci nezavisly a taky na tom, zda je ta mince dokonale symetricka. Pokud je to standartni priklad stredni skoly, tak se po vas nejspis chce toto:
0,5 je sance ze padne nejaka strana mince, jedno jaka, pokud je to jev zavisly, potom je to 0,5*0,5*0,5=0,5^3=0,125. Pokud zavisly neni, potom je jedno co padlo predtim, tedy sance je vzdy 50:50 nebo chte-li 1:1.
Offline
#3 27. 04. 2011 18:18
Re: pravděpodobnost při hodu 3 mincí
↑ Krezz:je to úloha z vysokoškolské statistiky.
V příkladě je tou mincí myšleno jaká strana té mince padne, ale o zbytku nemám tušení. Právě také nevim, zda jde o závislý nebo nezávislý jev. Ze zadání bych řekla, že spíše závislý, protože je napsáno padne-li a právě to padne-li mě nějak mate.
Offline
#4 27. 04. 2011 18:29
Re: pravděpodobnost při hodu 3 mincí
↑ dexka:
tak to se omouvám, pokud se jedná o vysokoškolský příklad tak je řešením využití binomického rozdělení.
Mě právě zmátlo to, že je to příklad v sekci střední škola, kde se tyto věci probírají pouze hodně jednoduše v kombinatorice.
Offline
#6 27. 04. 2011 19:20 — Editoval Krezz (27. 04. 2011 19:21)
Re: pravděpodobnost při hodu 3 mincí
↑ dexka:
klidně to sem napiš pokud si nejsi jistá. Tyhle příklady jsou opravdu typové, vyskytují se na všech VŠ nejspíš stejně.
Výpočet je snadný, v podstatě je uplně jedno jestli má padnout vždy stejná strana mince, nebo ta kterou zrovna vybereme, jelikož ty pravděpodobnosti v každem hodu že se trefime nebo netrefime jsou stejne, v okamžiku kdy bych rekl ze ta mince neni symetrická a že pada z 66% orel a 34 panna, potom by to uz melo smysl. Takze je to pouze počet hodu * 0,5^3 tedy nejakych 0,375. Jinej priklad bych mohl mit treba budu hazet 2x 2ma kostkama a jaka je sance ze hodim pokazde dve dvojky a pak se treba zeptam jaka je sance ze poprvne nehodim zadnou, podruhe jednu atd, tech variaci a mnoho.
Offline
#7 27. 04. 2011 19:29 — Editoval OiBobik (27. 04. 2011 19:31)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: pravděpodobnost při hodu 3 mincí
↑ dexka:
Já bych jev "padne-li poprvé líc, pak... " pochopil v souladu s výrokovou logikou jako jev: "poprvé nepadne líc nebo potřetí padne to stejné, co podruhé". Tedy řešením by byla pp=0,5 (odpovídá "nepadne poprvé líc") + 2*(0,5^3) (odpovídá jevům "líc líc líc", "líc rub rub").
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#8 27. 04. 2011 21:54
Re: pravděpodobnost při hodu 3 mincí
↑ Krezz: Tak tedy celá úloha zní: Hodíme třikrát mincí. Určete pravděpodobnost, že: a)padne poprvé líc; b) padne třikrát za sebou tatáž mince; c) padne-li poprvé líc, padne potřetí stejná mince jako podruhé.
a) jsem vypočítala 0,5
b) 0,25
ale c) mi dělá teda problém no. Ten zadaný líc mi totiž připadá jako podmínka, aby mohlo padnout to ostatní, a proto nevím jak s tím.
Offline
#10 27. 04. 2011 22:53
Re: pravděpodobnost při hodu 3 mincí
↑ Krezz: tě prkno, dokonce.. pro mě už je nejhorší poznat kdy co mám použít. nemáte nějaký materiál, který by mi od sebe odlišil tyhle možnosti? aby bylo přesně stanoveno kdy co mám jak počítat.. ta naše skripta jsou dobrá na čtení, ale rozdíl ve výběru výpočtu nepoznám..
jiank teda moc moc moc děkuji
Offline
#12 27. 04. 2011 23:16 — Editoval OiBobik (27. 04. 2011 23:38)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: pravděpodobnost při hodu 3 mincí
↑ Krezz:
Máš to b) nějak divně. Vždyť třikrát po sobě padne jedna barva = (padne třikrát líc) nebo (padne třikrát rub), oba dílčí jevy mají pp. 0,5^3 a dílčí pravděpodobnosti zřejmě sčítám, tudíž pp= 2*(0,5^3)=0,5^2=0,25
Pokud bys to chtěl v řeči binomického rozdělení, je to zkrátka 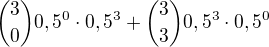
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#14 28. 04. 2011 00:05
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: pravděpodobnost při hodu 3 mincí
↑ dexka:
Jiná úvaha, stejně tak správná a je správný i výsledek. ; ))
Dá se na to třeba ještě dívat úplně klasicky středoškolsky:
vyhovují nám právě dvě ze všech uspořádaných trojic výsledků (čili rub rub rub, líc líc líc)
pp je počet vyhovujících výsledků lomeno počet všech možných výsledků, těch je 2^3 -> 
apod.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#15 28. 04. 2011 00:25
Re: pravděpodobnost při hodu 3 mincí
↑ OiBobik: máš pravdu, špatně sem dosadil. Měla tam být místo 1 0 a na druhou možnost sem jaksi zapoměl, tedy dvakrat. Omlouvám se.
Offline

