Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Complex no. (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 04. 2011 06:57
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Complex no.
(4) If  are distinct Complex no. such that
are distinct Complex no. such that  .then find value of
.then find value of 
Offline
- (téma jako vyřešené označil(a) byk7)
#2 28. 04. 2011 11:17 — Editoval musixx (28. 04. 2011 12:40)
Re: Complex no.
Clearly, a, b, and c are distinct from 1, and if one of them is zero, then also all others together with k are zero (EDIT: In the end, that is a contradiction with the condition that a,b,c are distinct complex numbers).
So let's assume all of them to be distinct from 0 and 1, and let's assume that such k exists.
If we compute c from 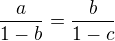 and from
and from  , and if we compare those two results, we have an equation
, and if we compare those two results, we have an equation  . We are looking for
. We are looking for  , so let's divide that equation with nonzero
, so let's divide that equation with nonzero  , and let's introduce a common trick "+1-1" to a fraction
, and let's introduce a common trick "+1-1" to a fraction  . That transforms our equation to
. That transforms our equation to 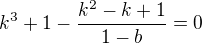 . Since
. Since 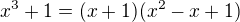 , we have
, we have 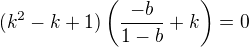 .
.
But 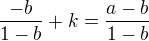 , and we assume
, and we assume  , so therefore
, so therefore  which gives
which gives 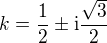 .
.
It is easy to verify that both solutions are possible.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Complex no. (TOTO TÉMA JE VYŘEŠENÉ)