Matematické Fórum

luboss8 · 03. 05. 2011 17:01

Ahojte,
mohli by ste mi prosím vás vysvetliť vzdialenosti? Chybal som v skole a nic neviem.
Dakujem

luboss8

Cheop · 03. 05. 2011 17:02

↑ luboss8:
Jaké vzdálenosti máš na mysli?

luboss8 · 03. 05. 2011 17:23

vzdialenosť priamky od bodu

Cheop · 03. 05. 2011 17:37 — Editoval Cheop (03. 05. 2011 17:44)

↑ luboss8:
Mášli zadaný bod $X=(x_0;\,y_0)$ a přímku $ax+by+c=0$ , pak vzdálenost bodu od přímky d se vypočte
dle vzorce: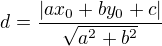
$d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}$
Příklad:
máme bod $X=(3;\,1)$ a přímku: $2x+y-5=0$ a máme určit vzdálenost tohoto bodu od uvedené přímky
Dosadíme do výše uvedeného vzorce a dostaneme:
V našem případě tedy: $a=2\\x_0=3\\b=1\\y_0=1\\c=-5$
$d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\\d=\frac{|2\cdot 3+1\cdot 1-5|}{\sqrt{2^2+1^2}}\\d=\frac{2}{\sqrt5}=\frac{2\sqrt 5}{5}$

Druhý způsob zdlouhavější je tento:
1) Určíš rovnici přímky, která je kolmá na zadanou přímku a prochází zadaným bodem
2) Určíš průsečík těch 2 přímek, jako řešení soustavy 2 rovnic o 2 neznámých
3) Hledaná vzdálenost je potom vzdálenost průsečíku a zadaného bodu jako vzdálenost 2 bodů

Hudler · 03. 05. 2011 17:43

Tak na toto téma zde určitě bude spousta vyřešených příkladů.

Za a) je na to vzorec

Za b) pro pochopení:

Vzdálenost bodu od přímky je definována jako nejmenší možná vzdálenost bodu od přímky - měří se po kolmici.

Máš přímku ax+by+c=0 ta má směrový vektor (a,b); z toho určíš normálový vektor - vektor kolmý - (-b,a) nebo (b,-a) (možné jsou lineární kombinace vektorů)

Dostaneš polotovar rce kolmé na přímku

bx-ay+d=0

za x,y dosadíš souřadnice bodu, jehož vzdálenost od přímky zjišťuješ (musí ležet na kolmici k dané přímce jejíž polotovar jsem uvedl)

Poté už jen určíš společný průsečík kolmice a přímky (soustava dvou rovnic o dvou neznámých) a dostaneš souřadnice průsečíku P. A spočítat vzdálenost bodu A (bod jehož vzdálenost od přímky zjišťujeme) od bodu P už je jednoduché.

luboss8 · 04. 05. 2011 10:42

Dakujem za odpovede :)

Matematické Fórum

#1 03. 05. 2011 17:01

Vzdialenosti

#2 03. 05. 2011 17:02

Re: Vzdialenosti

#3 03. 05. 2011 17:23

Re: Vzdialenosti

#4 03. 05. 2011 17:37 — Editoval Cheop (03. 05. 2011 17:44)

Re: Vzdialenosti

#5 03. 05. 2011 17:43

Re: Vzdialenosti

#6 04. 05. 2011 10:42

Re: Vzdialenosti

Zápatí