Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » perfect square polynomial (TOTO TÉMA JE VYŘEŠENÉ)
#1 29. 04. 2011 08:31
- stuart clark

- Příspěvky: 1015
- Reputace: 7
perfect square polynomial
does there exist a positive integer 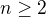 so that
so that 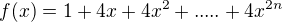 is a perfect square polynomial
is a perfect square polynomial
Offline
- (téma jako vyřešené označil(a) byk7)
#2 29. 04. 2011 11:16 — Editoval musixx (29. 04. 2011 11:41)
Re: perfect square polynomial
Since f(x) must be a perfect square polynomial, then all its roots must be multiple roots. In the same time, all those roots must be roots of f'(x) with a well-known consequency to their multiplicities.
Degree of f'(x) is 2n-1, and if f'(x) contained two distinct roots, then a degree of f(x) would be bigger than 2n -- a contradiction.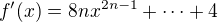 .
.
Therefore f'(x) must be of a form 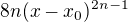 with the unique real root (consider complex conjugates to realize that the root must be a real one), and comparing the absolute terms, we have the only candidate
with the unique real root (consider complex conjugates to realize that the root must be a real one), and comparing the absolute terms, we have the only candidate ![kopírovat do textarea $x_0=-\sqrt[2n-1]{\frac1{2n}}$](/mathtex/f4/f4f62067af4d079df265b9f0aa07832c.gif) .
.
It is easy to see (verify by yourself) that since the absolute term of ![kopírovat do textarea $f(x)=4\(x+\sqrt[2n-1]{\frac1{2n}}\)^{2n}$](/mathtex/9e/9eec63a63aa91e00e99cb4c3fd6d2efb.gif) is
is 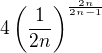 , then it is equal to 1 only if n=1.
, then it is equal to 1 only if n=1.
------
Can I ask who are you? You publish here more advanced questions from analysis and algebra, moreover in English which is not so common here... For sure, it is no problem. It is just my (maybe not only my) personal interest. I can remember that e.g. Marian, Rumburak, Pavel, and Pavel Brožek have answered your questions, as well.
Offline
#4 03. 05. 2011 09:17
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: perfect square polynomial
Thanks musixx for solving my question also thanks to all members to show interest on my questions.
and byk7 you are saying right I am from India.
Offline
#5 03. 05. 2011 19:55
Re: perfect square polynomial
↑ stuart clark: Can I ask you, too? How/when did you find this website?
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#6 04. 05. 2011 22:15
Re: perfect square polynomial
Let 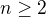 . Then
. Then 
Prove that  for any
for any 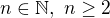 .
.
The sequence 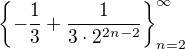 is decreasing therefore
is decreasing therefore
However, values of a perfect square polynomial can be only nonnegative real numbers. Hence  cannot be a perfect square polynomial.
cannot be a perfect square polynomial.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#7 05. 05. 2011 19:06
- stuart clark

- Příspěvky: 1015
- Reputace: 7
Re: perfect square polynomial
Actually I have got this site 2 months ago with the help of google search.
Thanks povel for explanation.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » perfect square polynomial (TOTO TÉMA JE VYŘEŠENÉ)
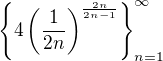 is a descending sequence
is a descending sequence