Matematické Fórum

Phate · 04. 05. 2011 23:48

Dobry vecer, moc casto se tu na neco neptam, spise se snazim pomahat, tak me snad neukamenujete, kdyz tu bude vice podotazek v jedne otazce. V moji priprave na maturitu jsem zakopl o tyto podotazky k integralum a moc si s nimi nevim rady:
muj postup, i kdyz je to spise loterie:
a) udelal bych f-ci, ktera pro interval <1;3> bude dirichletovou funkci a pro zbytek oboru nejakou hezkou spojitou derivovatelnou, ale nevim, jestli je to zrovna elegantni reseni.
b) tady bohuzel vubec netusim
c) rekl bych, ze takova funkce by nemusela existovat, ale usuzuji tak ciste z toho, ze nevim, jak a jestli vubec se daji neelementarni funkce derivovat
d) znovu bych volil dirichletovu funkcni, je to asi trochu jak tankem na komara, ale nevim, jestli v mem skromnem stredoskolskem aparatu vezi nejaka lepsi "placacka".

Dekuju predem za pomoc.

Alivendes

1) mohl by jsi nacpat pod odmocninu nějakou kvadratiuckou rovnici:
$\sqrt{x^2-4x+3}$
řešíš podmínku
${x^2-4x+3}>0$
$x\epsilon(-\infty,1>U<3,\infty)$
pro vnitřní interval není funkce definovaná, tak nemůže být ani žádnou primitivní funkcí

Alivendes

3) takových funkcí je spoustu, například $f(x)=e^{x^{2}}$

nebo $f(x)=sin(x^2)$

Tyhle funkce mají primitvní funkce, dokonce známe i graf, ale není možné danou primitivní funkci zapsat pomocí elementárních funkcí, například primitvní funkce k $f(x)=e^{x^{2}}$ je tzv. Gaussova křivka

Alivendes · 05. 05. 2011 08:37

2) Tyhle meze sedí pro funkci $F(x)=2^x$
$2^0=1$
$2^1=2$
funkci ted dostavame derivaci
$f(x)=(2^x)'=2^x ln2$

Pavel · 05. 05. 2011 11:23

↑ Alivendes:

1. může být Dirichletova funkce

2. Protože platí

$\int_{\underline{0}}^1 D(x)\,\text{d}x=0,\quad\int_{0}^{\overline{1}} D(x)\,\text{d}x=1,$

stačí upravit integrand tak, aby oba integrály vyšly tak, jak chceš.

3. jak bylo řečeno, např. 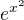$e^{x^2}$ .

4. opět Dirichletova funkce - horní a dolní integrály se nerovnají.

Phate · 05. 05. 2011 12:53

$\int_{\underline{0}}^1 D(x)\,\text{d}x=0,\quad\int_{0}^{\overline{1}} D(x)\,\text{d}x=1,$
Trochu stale nechapu, takze pokud budu mit funkci rostouci, tak se v tomto zapisu se bude ten prvni integral pocitat jako $\int_{\underline{0}}^1 D(x)\,\text{d}x=0=\int_{\underline{0}}^1 D(0)\,\text{d}x$ ? Je to jakoby, ze na intervalu <0;1> se vezme nejnizsi funkcni hodnota?

Matematické Fórum

#1 04. 05. 2011 23:48

Integraly, Riemannuv integral 1

#2 05. 05. 2011 08:18 — Editoval Alivendes (05. 05. 2011 08:40)

Re: Integraly, Riemannuv integral 1

#3 05. 05. 2011 08:20 — Editoval Alivendes (05. 05. 2011 08:23)

Re: Integraly, Riemannuv integral 1

#4 05. 05. 2011 08:37

Re: Integraly, Riemannuv integral 1

#5 05. 05. 2011 11:23

Re: Integraly, Riemannuv integral 1

#6 05. 05. 2011 12:53

Re: Integraly, Riemannuv integral 1

Zápatí