Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 05. 2011 22:26
Konvergence řady
Ahoj, mám problém s tímto příkladem  .
.
Mám 2 řešení vedoucí k různým výsledkům,
1. 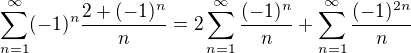 , druhá suma je
, druhá suma je
harmonická řada, a celkově řada diverguje . . .
2.  , řada pak z Leibnitzova kriteria konverguje . . .
, řada pak z Leibnitzova kriteria konverguje . . .
Nevím, v čem dělám chybu, ale ani pro jeden postup se mi nedaří najít protipříklad, který by ukázal, že daný krok je nekorektní.
Díky
pi = 3
Offline
- (téma jako vyřešené označil(a) Azeret)
#2 06. 05. 2011 22:51 — Editoval OiBobik (06. 05. 2011 22:58)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Konvergence řady
↑ Azeret:
Ahoj,
srovnávací kritérium má smysl jen u nezáporných řad - to tato není. 2. tedy nemá smysl.
Co se týče té jedničky, to se mi taky moc nelíbí - ono že něco rozložíš na třeba i dvě divergentní řady nic nedokazuje, snad jen, že řada nekkonverguje absolutně...
Osobně si myslím, že to bude divergovat, jen se k tomu snažím jenom najít správný argument.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#4 06. 05. 2011 23:01
Re: Konvergence řady
Díky, to proč je špatně číslo 1 už chápu. . .
A co s tou 2kou? - Jak píše OiBobik, nikde jsme žádné srovnávací kriterium pro
řady s obecnymi cleny nemeli, ale nedokazu najit protipriklad - kdyz vsechny prvky
v rade zvetsim a rada presto konverguje, je mozne aby nekonvergovala puvodni rada?
pi = 3
Offline
#5 06. 05. 2011 23:04 — Editoval OiBobik (07. 05. 2011 00:38)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Konvergence řady
↑ Azeret:
Na to ještě hezky odpověděl Jarro, než se smazal - tys tu řadu ani nezvětšil, tys zachoval sudé členy posloupnosti (kladné) a u lichých (záporných!) jsi zvětšil absolutní hodnotu - tedy sumu jsi rozhodně zmenšil(EDIT).
(stačí rozmyslet, že 2+(-1)^n je pro sudá n 3 a pro lichá 1 - ale u lichých je to celé násobeno -1, tedy záporné)
---------------------------------------
Skryto (nepřesné)
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#8 06. 05. 2011 23:41 — Editoval OiBobik (07. 05. 2011 00:56)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Konvergence řady
↑ Azeret:
Takže abych to sepsal trochu pořádně:
Součet nekonečné řady je definován jako limita posloupnosti částečných součtů - označme 
Pokud součet této řady (tedy tato limita) existuje, z teorie víme (a intuitivně je zcela zřejmé), že  (První člen jsme z řady "vyhodili").
(První člen jsme z řady "vyhodili").
(Pozn.: K platnosti stačí dokonce jen existence součtu řady na pravé straně, tedy "má-li pravá strana smysl, pak ta rovnost platí" - to je potřeba, jinak by celý ten důkaz byl nesmyslný)
Označme si částečné součty této nové řady 
Dokážeme nyní, že 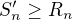 , kde
, kde  ... n-tý částečný součet
... n-tý částečný součet  , o níž víme, že diverguje.
, o níž víme, že diverguje.
Důkaz provedeme indukcí:
n=1.... zřejmě platí i 
n=2.... zřejmě platí
indukční krok 1 (pro lichá n, indukční předpoklad je:  ):
):
indukční krok 2 (pro sudá n, indukční předpoklad je:  ):
):
(idea důkazu je: pro lichá čísla dokazuju silnější tvrzení, ale stačí mi k tomu slabší, pro sudá dokazuju slabší, ale potřebuji k tomu silnější, a tak se to střídá pro libovolně velké n)
Nyní jsme tedy dokázali, že  , víme, že
, víme, že  ; z toho a lemmatu o policajtech plyne, že
; z toho a lemmatu o policajtech plyne, že  existuje a je také rovna
existuje a je také rovna  . Tím je divergence řady dokázána.
. Tím je divergence řady dokázána.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#9 07. 05. 2011 00:04 — Editoval Azeret (07. 05. 2011 00:04)
Re: Konvergence řady
↑ OiBobik:
wow, diky moc.
Jedna vec co mi neni uplne jasna, proc se vyndaval ten prvni clen souctu pred sumu? (nesel by udelat
obdobny dukaz jen by srovnavaci rada byla  ? )
? )
pi = 3
Offline
#10 07. 05. 2011 00:06 — Editoval OiBobik (07. 05. 2011 00:34)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Konvergence řady
↑ Azeret:
Nene, to se zdá, že by mohlo tak být, ale ve skutečnosti to nejde - lze to nahlédnout třeba tak, že aby to tak bylo, musí být předchozí člen větší nežli následující (nebo roven), tedy tak vysoká n musí splňovat nerovnici: ,
,
což žádné přirozené n nesplňuje.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#11 07. 05. 2011 00:08 — Editoval OiBobik (07. 05. 2011 00:58)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Konvergence řady
↑ Azeret:
Z formálních důvodů nešel - on ten první člen je totiž záporný a celou tu sumu posouvá (teď se tak dívám, že je tam chyba - ne 1/2, ale 1 se má odečítat, samozřejmě - jdu to spravit)(opraveno)
(co by teda šlo udělat, je nechat to od jedné, jak navrhuješ, pak je třeba to ale srovnávat s  - což by nevadilo, to jde do nekonečna stejně jako Rn : )) )
- což by nevadilo, to jde do nekonečna stejně jako Rn : )) )
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#12 07. 05. 2011 00:08
Re: Konvergence řady
↑ OiBobik:
jasny, chapu - diky moc (tohle by me nikdy nenapadlo . .. doufam, ze to jde nacvicit :) )
pi = 3
Offline
#13 07. 05. 2011 00:10 — Editoval OiBobik (07. 05. 2011 00:23)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Konvergence řady
↑ Azeret:
Nakonec jen upozornění - možná jsem to celé řešil zbytečně složitě. Třeba někdo ještě přijde a vymyslí jednodušší postup.
Btw: Mně by to před půl rokem taky ani nenapadlo, takže určitě jde ; )).
EDIT: Taky tam je přehozená parita u těch indukčních kroků, než jsem původně napsal - je to z důvodu toho posunutí. jdu to opravit. (opraveno)
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#14 07. 05. 2011 00:13
Re: Konvergence řady
↑ OiBobik:
neoznacim to tedy jeste jako vyresene - kdyby nekdo pripsal jednodussi postup vubec by mi
to nevadlo (tohle reseni nejde moc zobecnit na dalsi priklady a obavam se, ze pokud dostanu
obdobny priklad, nedokazu najit spravnou srovnavaci radu atd . ..)
pi = 3
Offline
#15 07. 05. 2011 00:22 — Editoval OiBobik (07. 05. 2011 00:32)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Konvergence řady
↑ Azeret:
OK. Já mám dokonce celkem silný pocit, že to nějak snáze půjde (něco podobného jsme velmi pravděpodobně dělali na cvičení a takovéto obludy tam cvičící neprezentoval, pokud se pamatuji). Nicméně aspoň si myslím, že je to teď správně.
_________________________________________________________________________
Ono asi obecně, když ti někdo zadá řadu, která se tváří na Leibnize, ale je jenom v takovém "detailu", jako je ta monotonie, nevyhovující, je to přinejmenším dobrý důvod k ostražitosti.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#16 07. 05. 2011 11:47 — Editoval fordox (07. 05. 2011 11:47)
- fordox
- Příspěvky: 29
Re: Konvergence řady
Zdravim, Naprostou nahodou jsem tento priklad nasel vyreseny v ucebnici, takze mohu poskytnout alternativni reseni...
Obecny clen řady se dá přepsat na : ((-1)^n)* (2*n) + 1*n. První řada je konvergentni podle leibnitzova kriteria, a druha rada diverguje... Pouzijeme- li vetu o aritmetice limit na posloupnosti castecnych souctu zjistime, ze zkoumana je divergentni.
Offline
#17 07. 05. 2011 12:14
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Konvergence řady
↑ fordox:
Aha, tak v tom případě řešení číslo 1 ↑ Azeret: bylo dobře.
Tak to se omlouvám, vypadalo to podezřele : )) (resp. spletl jsem si to s "důkazy" divergence takovými, kdy se řada rozdělí na jednu jdoucí k minus nekonečnu a druhou k plus nekonečnu).
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#18 07. 05. 2011 21:53
Re: Konvergence řady
↑ OiBobik:
jaj, nu co se da delat - spatne na tom je, ze jsi me v pohode presvedcil o tom, ze to je spatne - mam v tom ocividne pekny gulas . ..
kazdopadne diky moc - i tak mi to hodne pomohlo . . . .
pi = 3
Offline
 - tím bychom měli divergentní minorantu a naše řada by pak už divergovala.
- tím bychom měli divergentní minorantu a naše řada by pak už divergovala. , tedy
, tedy  ; to ovšem zase trochu zapáchá závorkováním, ovšem alespoň to ukazuje, že existuje podposloupnost částečných součtů, která roste alespoň tak rychle jako divergentní posloupnost
; to ovšem zase trochu zapáchá závorkováním, ovšem alespoň to ukazuje, že existuje podposloupnost částečných součtů, která roste alespoň tak rychle jako divergentní posloupnost 
 monotonni . . . coz by pro velka
monotonni . . . coz by pro velka  mohlo byt?
mohlo byt?