Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Základní škola
- » Pythagorova věta-Opsaná kružnice kolem obdelníku (TOTO TÉMA JE VYŘEŠENÉ)
#1 02. 06. 2008 15:14
- disconnect
- Zelenáč
- Příspěvky: 5
- Reputace: 0
Pythagorova věta-Opsaná kružnice kolem obdelníku
Zdravim...Asi zejtra budu zkoušený z této pro mne "nemožné" věci...Bude obdelník o (např.) stranách a=5 b= 7 a kolem něj bude opsaná kružnice. Užitím Pythagorovi věty musím spočítat poloměr kružnice. Ví někdo jak na to?:)
Offline
#2 02. 06. 2008 15:44
Re: Pythagorova věta-Opsaná kružnice kolem obdelníku
Samozřejmě, je to velice jednoduché.
Narýsuješ obdélník, najdeš těžiště (průsečík úhlopříček).
Kružnice má střed v onom těžišti a poloměr je půlka z úhlopříčky.
Početně je to podle pythagorovy věty takto: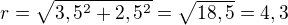
V podstatě jde o to, že si najdeš pravoúhlý trojúhelík s odvěsnami a/2 a b/2 a přeponou e/2 (polovina úhlopříčky). Ono e/2 je potom hledaný poloměr opsané kružnice.
oo^0 = 1
Offline
#3 02. 06. 2008 15:53
Re: Pythagorova věta-Opsaná kružnice kolem obdelníku
Poloměrem kružnice opsané obdélníku bude polovina délky úhlopříčky obdélníka.
Pokud budou rozměry obdélníka:
jedna strana = a
druhá strana = b
pak poloměr kružnice opsané r bude (z Pythagorovy věty)
r = sqrt(a^2+b^2)/2
Slovně:
Poloměr bude druhá odmocnina (z a na druhou plus b na druhou) lomeno dvěma
Offline
#4 02. 06. 2008 16:03
- disconnect
- Zelenáč
- Příspěvky: 5
- Reputace: 0
Re: Pythagorova věta-Opsaná kružnice kolem obdelníku
A pokud by to byla kružnice vepsaná ve stejném obdelníku tak by to bylo jak?
Offline
#7 02. 06. 2008 16:57
- disconnect
- Zelenáč
- Příspěvky: 5
- Reputace: 0
Re: Pythagorova věta-Opsaná kružnice kolem obdelníku
No to sem vedel:D Ale jestli na to neni nejakej slozitej vzorec pres tu pythagorovku...Jinak jak by to bylo u sestiuhelniku ktery ma napriklad stranu 5cm a kolem neho opsana kruznice?:D Musim znat vsechny pripady nez me ten typek vyzkousi:D
Offline
#8 02. 06. 2008 17:10
Re: Pythagorova věta-Opsaná kružnice kolem obdelníku
↑ disconnect:
Kdyby to byl pravidelný šestiúhelník, tak tam jsou strany stejně dlouhé jako poloměr kružnice opsané, nebo ne?
Offline
#10 02. 06. 2008 19:59
- disconnect
- Zelenáč
- Příspěvky: 5
- Reputace: 0
Re: Pythagorova věta-Opsaná kružnice kolem obdelníku
No to je hezké že to je stejné, ale já to budu muset nějak podle pyth. věty spočítat:(
Offline
#11 02. 06. 2008 20:27
Re: Pythagorova věta-Opsaná kružnice kolem obdelníku
↑ Cipis:
Fíha, abych řekl pravdu, tak nemám tušení. Tohle jsem si jen nějak pamatoval ze školy, ale podrobnosti už nevím (asi jsem si to říkali, ale už teď se stydím, že si to nepamatuji). V každém příapdě se nechám rád poučit, pokud to bude pro mne srozumitelné (jako laika, tzn. po lopatě).. ;)
Offline
#12 02. 06. 2008 20:42 — Editoval Cipis (02. 06. 2008 23:43)
Re: Pythagorova věta-Opsaná kružnice kolem obdelníku
Máme kružnici o poloměru r
Do této kružnice vepíšeme pravidelný šestiúhelník. (Jako bychom šestiúhelníku opsali kružnici)
Pokud jednotlivé strany šestiúhelníku spojíme se středem kružnice
dostaneme 6 trojúhelníků. (shodných)
Te jeden trojúhelník bude mít 2 strany o velikosti r a zatím třetí stranu o neznámé velikosti
Celkový úhel kruhu je 360 stupňů. Protože těch trojúhelníků je šest pak středový úhel, který připadá na jeden trojúhelník
je 360/6 = 60 stupňů
Máme tedy rovnoramenný trojúhelník, jehož ramena mají délku r (poloměr kružnice opsané) a tato ramena svírají úhel 60 st.
Na další 2 úhly v jednom trojúhelníku zbývá dohromady 180-60=120 stupňů. Protože trojúhelník je rovnoramenný, pak
na úhly při třetí straně musí být stejné tj. jeden úhel i druhý úhel musí mít velikost 120/2 = 60 stupňů
Teˇjsme právě zjistili, že všechny úhly v trojúhelníku mají 60 stupňů a to tedy znamená, žeten trojúhelník je rovnostranný.
Rovnostranný trojúhelník jak už sám název napovídá má všehny strany stejně dlouhé.
Protože na začátku měly 2 strany trojúhelníka velikost poloměru kružnice opsané má i třetí strana trojúhelníku velikost r
a to tedy znamená, že:
strana šestiúhelníku má stejnou velikost jako poloměr kružnice tomuto šestiúhelníku opsaná
Offline
#14 02. 06. 2008 21:20
Re: Pythagorova věta-Opsaná kružnice kolem obdelníku
↑ Cipis:↑ Ivana:
Pěkné, musím Vám oběma poděkovat, tohle se bude určitě někdy hodit a rozhodně to je zajímavé čtení .), snad to pomohlo i ↑ disconnect:.
Ještě jednou děkuji (a to včetně toho, že jste to dokázali napsat takto jednoduše :))
Offline
#15 02. 06. 2008 21:33 — Editoval Cipis (02. 06. 2008 23:46)
Re: Pythagorova věta-Opsaná kružnice kolem obdelníku
Obecně platí pro pravidelné n - úhelníky vztahy: n>2(dají se odvodit)
r - poloměr kružnice opsané
R - poloměr kružnice vepsané
a - délka strany n - úhelníka
n - počet vrcholů
r = a/(2*sin(180/n))
a = 2r*sin(180/n)
R = a*cotg(180/n)/2
R = r*cos(180/n)
Offline
#16 03. 06. 2008 17:43
- disconnect
- Zelenáč
- Příspěvky: 5
- Reputace: 0
Re: Pythagorova věta-Opsaná kružnice kolem obdelníku
Ehm...Diky moc, sice sem to neudelal ale fakt moc dekuju...
Offline
#17 03. 06. 2008 19:26
Re: Pythagorova věta-Opsaná kružnice kolem obdelníku
↑ disconnect:Máš ten příklad , který si neudělal ? Jestli ano , napiš ho sem .Vždy't chybami se člověk učí . :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
Stránky: 1
- Hlavní strana
- » Základní škola
- » Pythagorova věta-Opsaná kružnice kolem obdelníku (TOTO TÉMA JE VYŘEŠENÉ)

